
<ミツバチの巣の秘密>
ミツバチは巣を作る際に、材料を最小限におさえて可能な限りの広い空間を作ろうとしているようです。
丸や八角形では隙間ができますし、三角形や四角形では面積が小さくなり、六角形が最も効率が良いことがわかります。
そして、この六角形を並べた形のことをハニカム構造と呼ぶそうです。構造的にとても丈夫な形として知られ、飛行機の翼や人工衛星の壁にも応用されているそうです。
羽化後1週間ほどたった働きバチは、腹部ロウ腺が発達してきて、ロウを分泌するようになります。そして、ハチの巣はロウで作られた小部屋の集合体です。小部屋は、幼虫を育てたり、ハチミツや花粉を貯蔵するためにつかわれます。ハチの巣は、巣版の両面に小部屋が作られ、表と裏が半分ずつ重なり、薄いロウで仕切られていて、ハチミツを蓄えるほどしっかりと丈夫にできているそうです。
<問題>
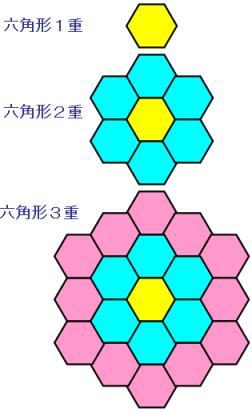
上の正六角形の図を見てください。正六角形を2重に並べると辺の合計数は30本、3重に並べると辺の合計数は72本になります。
ここで問題です。
正六角形を5重にならべると、辺の合計数は何本になるでしょうか。