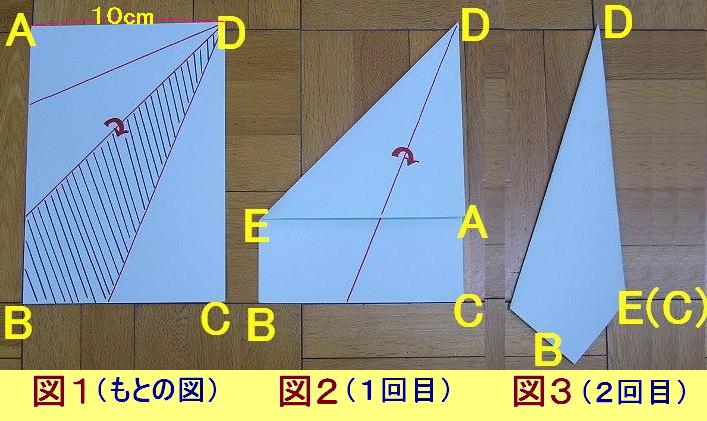
丂僐僺乕梡巻傗嫵壢彂偼偁傞婯奿偵婎偯偄偨挿曽宍偱偡丅偙偺挿曽宍偺巻ABCD傪丄師偺傛偆偵俀夞愜傝傑偟偨丅
亂侾夞栚亃10cm偺曈AD傪曈CD偵廳偹偰愜傞丅曈AB偲愜傝栚偲偺岎揰傪E偲偟傑偡丅
亂俀夞栚亃愜傝栚ED傪曈CD偵廳偹偰愜傝傑偡丅
丂偙偺傛偆偵愜傞偲丄揰俤偲揰C偑傄偭偨傝廳側傝傑偡丅忋恾侾乣恾俁偼愜偭偰偄偔條巕傪帵偟偨傕偺偱偡丅
偙偙偱栤戣偱偡丅
恾俁偺巐妏宍偮傑傝恾侾偺幬慄傪偮偗偨巐妏宍偺柺愊傪媮傔偰偔偩偝偄丅
丂偙偺栤戣偺廲偲墶偺斾棪偼梡巻僒僀僘偵嵦梡偝傟偰偄傞懠丄寶暔側偳偵巊傢傟偰偄傑偡丅堦曈偲懠曈偑偙偺斾偲側傞挿曽宍偼丄敀嬧挿曽宍乮敀嬧斾乯偲屇偽傟偄傑偡丅
丂偙偺斾偑梡巻僒僀僘偲偟偰梡偄傜傟偰偄傞棟桼偼丄梡巻傪挿庤曽岦偵敿暘偵偟偨偲偒偵尦偲憡帡偺宍忬偲側傞偨傔丄戝偒側梡巻傪愗傞偩偗偱婯奿偵揔崌偟偨彫偝側梡巻偑摼傜傟傞偨傔偱偡丅
丂傑偨丄擔杮寶抸偵偍偗傞儌僕儏乕儖偺1偮偲偟偰敀嬧斾偑梡偄傜傟偰偄傑偡乮椺丗朄棽帥偺屲廳搩偺搳塭恾偺抁曈偲挿曈偺娭學乯丅傑偨戝岺摴嬶偺巜嬮乮偝偟偑偹乯傪巊偭偨悺朄嵦傝傕偙偺敀嬧斾偑棙梡偝傟傑偡丅