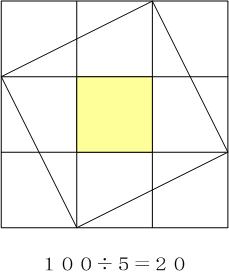
上図は一辺10cmの正方形ABCDの色紙です、そして、点EFGHはそれぞれの辺の中点です。これを、上図のように折って、四角形EFGHと四角形IJKLを作りました。
ここで問題です。
四角形EFGHは四角形IJKLより何cm2大きいでしょうか。
|
|
|
<問題> 上図は一辺10cmの正方形ABCDの色紙です、そして、点EFGHはそれぞれの辺の中点です。これを、上図のように折って、四角形EFGHと四角形IJKLを作りました。 ここで問題です。 四角形EFGHは四角形IJKLより何cm2大きいでしょうか。 |
<正解者一覧表>
| 正解者順位 | name | メール到着日時 | 備 考 |
| 1 | マッキー27 さん | 2008/8/1 0:01 | 愛知県 |
| 2 | NAMPOTのPOT さん | 2008/8/1 0:02 | |
| 3 | こば さん | 2008/8/1 0:03 | |
| 4 | nak さん | 2008/8/1 0:06 | 鹿児島県 |
| 5 | Mr.ダンディ さん | 2008/8/1 0:07 | 大阪府 |
| 6 | ローラ さん | 2008/8/1 0:08 | |
| 7 | スモークマン さん | 2008/8/1 0:50 | 体の芯に熱がこもってる ^^;; |
| 8 | エトランゼ さん | 2008/8/1 1:01 | |
| 9 | ma-mu-ta さん | 2008/8/1 1:11 | 東京都 |
| 10 | ルルゥ さん | 2008/8/1 3:09 | |
| 11 | いちもく さん | 2008/8/1 4:44 | 立川市 |
| 12 | タカピー さん | 2008/8/1 6:51 | 中学生 |
| 13 | 巷の夢 さん | 2008/8/1 6:55 | 宮城県出身 |
| 14 | SaiSai さん | 2008/8/1 9:45 | 大阪市:プログラマー |
| 15 | y.okada さん | 2008/8/1 11:43 | |
| 16 | KAZU さん | 2008/8/1 14:53 | 熊本 |
| 17 | 経友会の進作 さん | 2008/8/1 16:17 | 京都府木津川市・70歳 |
| 18 | algebra さん | 2008/8/1 17:30 | 神奈川県 |
| 19 | A6 さん | 2008/8/1 19:20 | |
| 20 | ゴンとも さん | 2008/8/1 22:24 | 豊川市 |
| 21 | heta さん | 2008/8/1 23:42 | 京都府 |
| 22 | ラスカマン さん | 2008/8/2 0:42 | 静岡県伊豆半島 |
| 23 | banyanyan さん | 2008/8/2 1:51 | 京都府 |
| 24 | akira さん | 2008/8/2 7:13 | 東京都 |
| 25 | まいすた さん | 2008/8/2 9:53 | |
| 26 | lapin さん | 2008/8/2 10:45 | 大阪府交野市 |
| 27 | teki さん | 2008/8/2 13:53 | 大阪府 |
| 28 | ヤマラー さん | 2008/8/2 17:34 | |
| 29 | kasama さん | 2008/8/2 17:37 | 和歌山県プログラマ |
| 30 | fisherman さん | 2008/8/2 20:12 | 豊岡市・塾講師 |
| 31 | なにわ さん | 2008/8/2 21:11 | 西宮市 |
| 32 | uchinyan さん | 2008/8/3 14:05 | 東京都 |
| 33 | 数学爺 さん | 2008/8/3 14:19 | 数学爺 |
| 34 | 省ちゃん さん | 2008/8/4 8:43 | 静岡県元中学数学教師 |
| 35 | 湘南人 さん | 2008/8/4 12:11 | 神奈川県 |
| 36 | やぶコウノトリ さん | 2008/8/4 13:23 | 兵庫県 |
| 37 | 魔法使いサリン さん | 2008/8/4 15:30 | 滋賀県 |
| 38 | 川上智弘 さん | 2008/8/4 21:51 | 兵庫県出身 |
| 39 | みかん星人 さん | 2008/8/4 22:17 | |
| 40 | 宮 さん | 2008/8/4 22:33 | 鹿児島放送大学学生 |
| 41 | ミルクルミ さん | 2008/8/5 15:37 | |
| 42 | 阿修羅 さん | 2008/8/5 18:30 | 長野県小学校教諭 |
| 43 | 元気モリモリ さん | 2008/8/5 20:00 | |
| 44 | おとおさん さん | 2008/8/5 21:15 | |
| 45 | take さん | 2008/8/5 22:01 | |
| 46 | shinji-y さん | 2008/8/5 22:04 | |
| 47 | シュウ さん | 2008/8/6 0:23 | |
| 48 | SSO さん | 2008/8/6 18:17 | 長野市出身 |
| 49 | りょうた さん | 2008/8/7 4:45 | 東京都 |
| 50 | 浪人 さん | 2008/8/8 3:05 | 岩手県大船渡市 |
| 51 | りーくん さん | 2008/8/8 19:23 | 埼玉県 |
| 52 | 都留文太 さん | 2008/8/10 12:48 | 群馬県 |
| 53 | 信三 さん | 2008/8/11 5:34 | シリコンバレーの住人 |
| 54 | tomo2 さん | 2008/8/11 11:31 | 東京都 |
| 55 | 梨里沙11 さん | 2008/8/11 16:29 | 小6です!! |
| 56 | ハセヲ さん | 2008/8/11 21:44 | 大阪府在中高校1年生 |
| 57 | nakakun さん | 2008/8/12 0:32 | 神奈川県 |
| 58 | 中3(復活)!?航空アニマル さん | 2008/8/12 19:38 | 東京都26市内中学3年生 |
| 59 | あり さん | 2008/8/15 13:14 | |
| 60 | 風の旅人 さん | 2008/8/15 14:16 | 愛媛県出身、大学生 |
| 61 | a さん | 2008/8/16 12:11 | |
| 62 | ぴーしゅん さん | 2008/8/19 11:37 | |
| 63 | とし さん | 2008/8/19 13:44 | |
| 64 | 鞍馬の天狗 さん | 2008/8/19 15:07 | 大阪府中二 |
| 65 | スカピン さん | 2008/8/19 22:44 | 田舎 |
| 66 | テモ さん | 2008/8/24 18:38 | 広島市の美鈴が丘 |
| 67 | i さん | 2008/8/26 14:11 | 神奈川県 |
| 68 | taka さん | 2008/8/26 22:56 | |
| 69 | 君の船 さん | 2008/8/28 11:48 | |
| 70 | ちんにくマン3世 さん | 2008/8/29 14:39 |
こたえは、30cm2でした。