「今月の問題」　第１０８回　（平成２０年９月）

　

＜問題＞

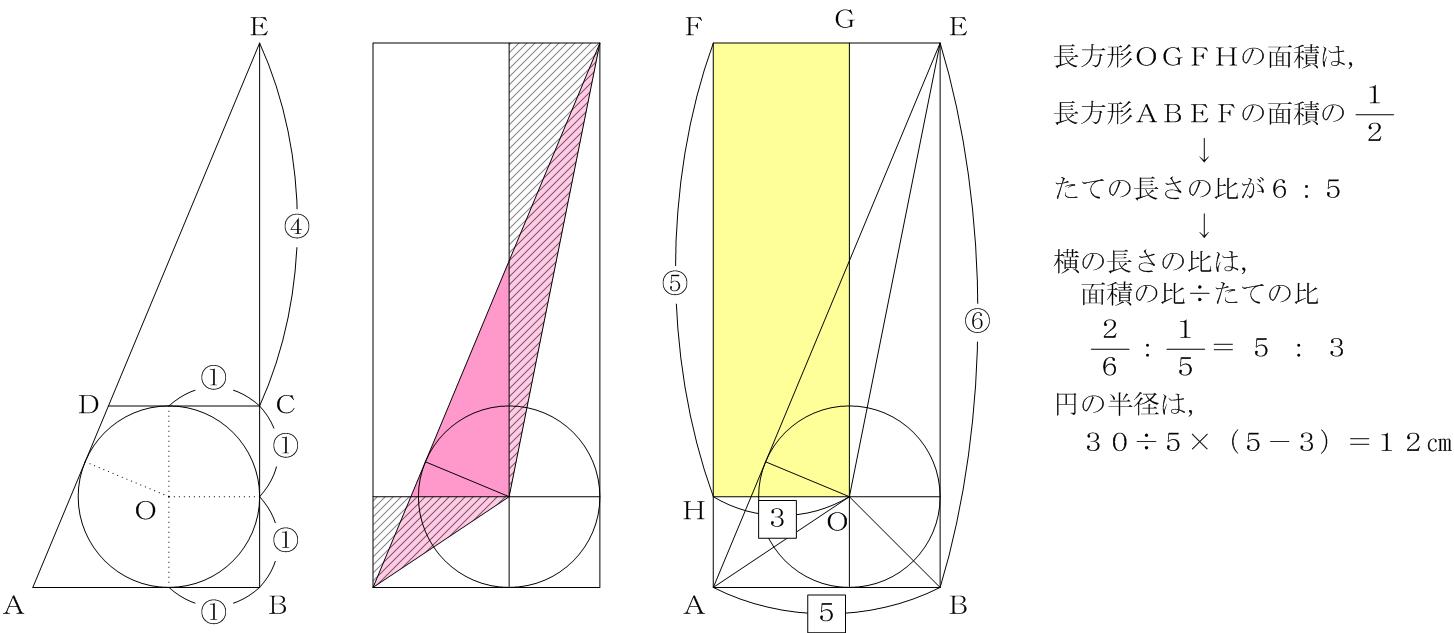
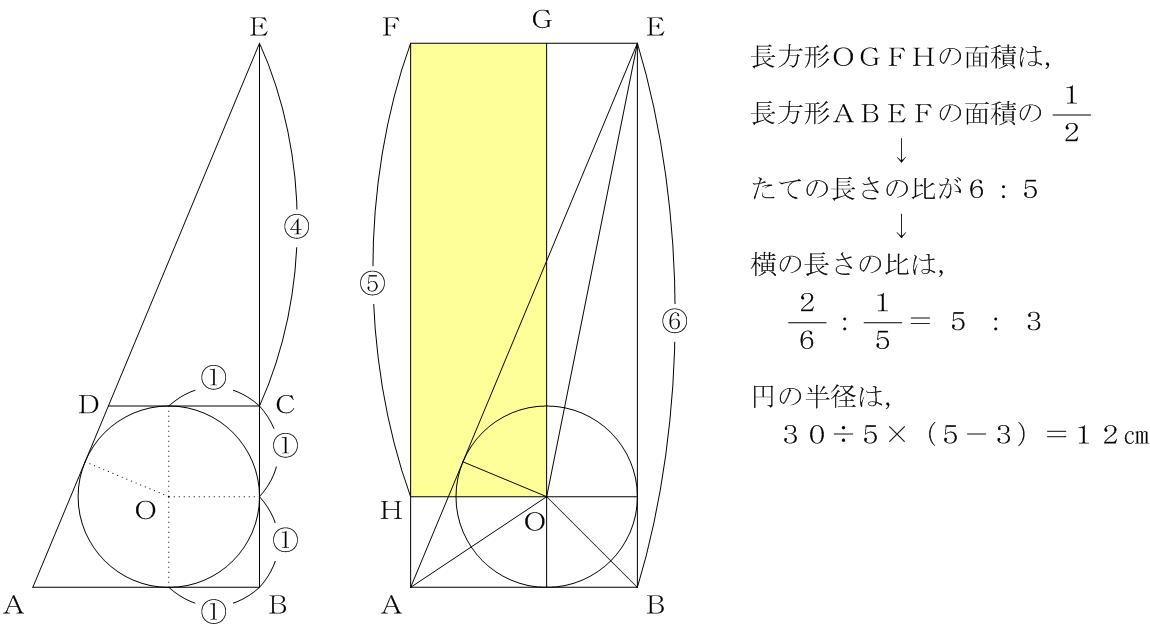
　左図を見てください。∠Bと∠Cが90°である四角形ＡＢＣＤがあります。そして、辺の長さを計るとABが30cmであり、DCが20cmです。

ここで問題です。

四角形ABCDに内接する青色の円の直径の長さはいくらになるでしょうか。

　

＜ミニ知識：○△平均＞
　（20＋30）÷2＝25は相加平均といわれます。SQR（20×30）＝24.495は相乗平均ともいわれます。
そして、この問題の円の直径は、20と30の○△平均になります。

＜正解者一覧表＞　 　　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１SSO　さん2008/9/1　0:03　
　２マッキー２７　さん2008/9/1　0:11長野県　
　３Ｍｒ．ダンディ　さん2008/9/1　0:13大阪府　
　４ma-mu-ta　さん2008/9/1　0:34東京都　
　５エトランゼ　さん2008/9/1　1:24埼玉県　
　６いちもく　さん2008/9/1　5:13立川市　
　７浪人　さん2008/9/1　5:39岩手県大船渡市　
　８巷の夢　さん2008/9/1　7:13宮城県出身　
　９algebra　さん2008/9/1　8:18神奈川県　
１０NAMPOTのPOT　さん2008/9/1　8:59　
１１SaiSai　さん2008/9/1　10:04大阪市・プログラマ　
１２魔法使いサリン　さん2008/9/1　11:40滋賀県　
１３ちぐれ　さん2008/9/1　21:00ふくすま　
１４なにわ　さん2008/9/1　21:20西宮市　
１５宮　さん2008/9/1　21:38鹿児島県放送大学学生
１６ゴンとも　さん2008/9/1　22:12豊川市　
１７阿修羅　さん2008/9/1　22:12長野県小学校教諭　
１８uchinyan　さん2008/9/1　22:19東京都　
１９teki　さん2008/9/1　23:09大阪府　
２０ラスカマン　さん2008/9/1　23:10静岡県伊豆半島　
２１godspirit　さん2008/9/2　4:15埼玉県出身　
２２fisherman　さん2008/9/2　8:16豊岡市　
２３信三　さん2008/9/2　9:51シリコンバレーの住人
２４ banyanyan　さん2008/9/2　12:03京都府
２５理科ちゃんマン　さん2008/9/2　15:58理科の塾講師　
２６スモークマン　さん2008/9/2　18:1018歳の錦織圭惜しかった
２７数学爺　さん2008/9/2　17:03神奈川県　
２８川上智弘　さん2008/9/2　20:11兵庫県　
２９経友会の進作　さん2008/9/2　20:55京都府木津川市・70歳
３０ まいすた　さん2008/9/2　21:23　
３１中3(復活)!?航空アニマル　さん2008/9/2　23:07東京都26市内中学3年生
３２おとおさん　さん2008/9/3　0:15　
３３oguchan1　さん2008/9/3　0:44　
３４やぶコウノトリ　さん2008/9/3　11:32兵庫県　
３５川村高雅　さん2008/9/3　11:41神奈川県　
３６nak　さん2008/9/3　14:31鹿児島県　
３７tomo2　さん2008/9/3　16:31東京都　
３８A1　さん2008/9/3　18:29滋賀県　
３９風の旅人　さん2008/9/3　21:13愛媛県出身、みかん大好き
４０元気モリモリ　さん2008/9/4　18:42　
４１ルルゥ　さん2008/9/4　21:02新潟市
４２省ちゃん　さん2008/9/6　16:08元中学数学教師静岡県
４３タカピー　さん2008/9/6　17:51中学生　
４４KAZU　さん2008/9/8　9:26熊本　
４５あしゅら　さん2008/9/9　20:03　
４６lapin　さん2008/9/9　21:51大阪府交野市
４７kasama　さん2008/9/9　22:36和歌山県プログラマ
４８勇水　さん2008/9/9　23:26高知　
４９ゆうり　さん2008/9/11　20:10　
５０K村　さん2008/9/11　21:53埼玉県　
５１YAMATO　さん2008/9/12　1:33大阪在中の高校一年生
５２ りーくん　さん2008/9/15　23:02埼玉県
５３室岡　さん2008/9/17　18:17長野県　大学生
５４小宮　さん2008/9/19　16:18　
５５モニカ7　さん2008/9/20　23:00　
５６hankai　さん2008/9/29　23:24干物の国
５７ぴゅ−しゅん　さん2008/9/30　8:15　

答えは、２４cmでした。

[107] Re:[104] 算数 投稿者：banyanyan 投稿日：2008/09/19(Fri) 02:14 [返信]

http://banyanyan.up.seesaa.net/image/susanchallenge108-2420-20C4C9B2C3.jpg

質問があったので図を追加してみました。これで面積が１／２
であることがわかっていただけるのではないでしょうか。

http://banyanyan.up.seesaa.net/image/susanchallenge108-24.jpg

　
[106] 無題 投稿者：むぺむぺ 投稿日：2008/09/11(Thu) 20:41 [返信]

皆さんエレガントな方法で解いていますね。
私は、
AD=√(100+4r^2)と強引に持っていき、
あとは力技で三平方を使いました。

修業が足りませんね。

　
[105] 三角形で解きました。 投稿者：三日月キリン 投稿日：2008/09/05(Fri) 21:42 [返信]

既に出てますね。

相加相乗平均とか10年ぶりくらいに聞きましたｗ


　
[104] 算数 投稿者：banyanyan 投稿日：2008/09/04(Thu) 01:09 [返信]

算数で解くとこんな感じでしょうか。

延長して三角形を作り、その面積を考えました。

http://banyanyan.up.seesaa.net/image/susanchallenge108-24.jpg

　
[103] う〜〜ん 投稿者：理科ちゃんマン 投稿日：2008/09/02(Tue) 17:33 [返信]

三平方を使わずに算数で解きたいですねぇ。
もうしばらく考えてみます。

　
[102] いい問題です。 投稿者：西面　敏明 投稿日：2008/09/02(Tue) 09:22 [返信]

BC=2aとおいて、１点から引いた円に引いた接線の長さは等しいことを使って各接点をそれぞれE、F、G、Hとおきます。そのことからAD＝50-2aとなります。
次にDからABに対して垂線を下ろしその足をIとすると直角三角形DAIができます。AI=10　DI＝2a　3平方の定理を使って
a＝12　よって　直径は24cmになりました。
中学数学の方法で解きました。このところ割にすぐ解けております。今後ともよろしく

　
[101] 面倒な解法 投稿者：宮 投稿日：2008/09/01(Mon) 21:57 [返信]

私は、全体を直角三角形にして考えました。
そうすると、問題は直角三角形の内接円の直径を求める問題となります。三角形の面積より答えを導きます。
まず、CB=Xとします。点D・Cを延ばした交点をEとすると相似の三角形の比よりEB=3X。各辺と円の半径を高さとする三角形の和と全体の三角形の面積が等しいことを利用して等式を作りました。
30×X÷2÷2＋3X×X÷2÷2＋√900＋9X2乗×X÷2÷2＝30×3X÷2
X(円の直径）＝24

　
[100] 確かに 調和平均！ 投稿者：Ｍｒ．ダンディ 投稿日：2008/09/01(Mon) 01:01 [返信]

ＡＢ＝ａ ,ＤＣ＝ｂ ,半径＝ｒ とおいて[99]の回答と同じことをすると
確かに　1/ｒ＝1/ａ＋1/ｂ　という式が導かれ調和平均になることが確かめられました。

20cm,30cmのときに限らず調和平均になるのですね。（よくこういうことに気が付かれましたね。感心致します）

　
[99] 私の解法 投稿者：Ｍｒ．ダンディ 投稿日：2008/09/01(Mon) 00:35 [返信]

ＤからＡＢへ下ろした垂線をＤＨとします。

１点から引いた２本の接線の長さが等しいことをつかって
ＡＤ＋ＢＣ＝ＡＢ＋ＤＣ＝50 (cm)

△ＡＤＨにおいて
円の半径をｒ(cm)とすると　ＤＨ＝ＣＢ＝2ｒ (cm)
ＡＤ＝50−ＢＣ＝50−2ｒ (cm)
またＡＤ＝30-20＝10 (cm)
よって、三平方の定理より　(2ｒ)^2＋10^2＝(50−2ｒ)^2
これを解いて　ｒ＝12
答えは直径だから２４ｃｍとなりました。

以上完全な数学による解法ですが、算数での解法はあるのかな？

　
[98] 調和平均 投稿者：SSO 投稿日：2008/09/01(Mon) 00:22 [返信]

調和平均のようですね。(^^)