「今月の問題」　第１１０回　（平成２０年１１月）

　

＜問題＞

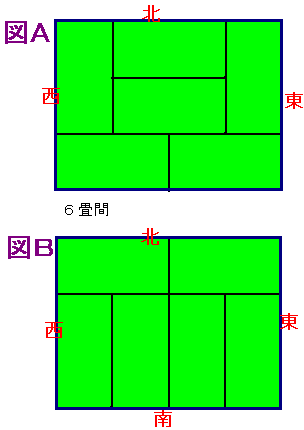
　よしお君の家では、６ 畳の和室の畳を替えることにしました。図Ａや図Ｂのように敷けます。
ここで問題です。
６畳の和室の畳の敷く方法は、何種類あるでしょうか。

　

＜ミニ知識＞
現実には古くから次のような条件で敷かれるので、図Ａのように敷き方は決まってくるようです。
@４枚の畳の角が１か所に集まらないようにする。
　⇒４つの角が集まった点が「シニメ」という言葉を連想させる
A部屋を上下または左右に二等分する線が入らないようにする。
　⇒2等分すると「キレル」「ワカレル」に通じ縁起が悪い

＜正解者一覧表＞　 　　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１ルルゥ　さん2008/11/1　0:09新潟市　
　２Ｍｒ.ダンディ　さん2008/11/1　0:19大阪府　
　３algebra　さん2008/11/1　0:25神奈川県
　４ma-mu-ta　さん2008/11/1　1:42東京都　
　５いちもく　さん2008/11/1　6:52立川市　
　６NAMPOTのPOT　さん2008/11/1　9:24　
　７男はつらいよ　さん2008/11/1　9:41　
　８あっくん　さん2008/11/1　10:34神戸市垂水区　
　９信三　さん2008/11/1　11:19ゴールデンゲイトパークの隠居　
１０スモークマン　さん2008/11/1　11:52人も赤・黄に染まったり...^^
１１hassy　さん2008/11/1　13:33さいたま　
１２teki　さん2008/11/1　15:23大阪府　
１３鞍馬の天狗　さん2008/11/1　17:08　
１４中島　淳　さん2008/11/1　17:14群馬　
１５とおりすがりのミズ　さん2008/11/1　20:40　
１６なにわ　さん2008/11/1　20:49西宮市　
１７fisherman　さん2008/11/1　21:04豊岡市・塾講師　
１８oguchan1　さん2008/11/1　21:50　
１９経友会の進作　さん2008/11/1　22:02京都府木津川市・70歳　
２０nak　さん2008/11/1　22:30鹿児島県　
２１ラスカマン　さん2008/11/1　22:32静岡県伊豆半島　
２２ まいすた　さん2008/11/1　23:02作曲家　
２３tomo2　さん2008/11/2　0:08東京都　
２４りーくん　さん2008/11/2　10:15埼玉県　
２５浪人　さん2008/11/2　17:50岩手県大船渡市
２６uchinyan　さん2008/11/2　18:27東京都　
２７マッキー２７　さん2008/11/2　23:57愛知県　
２８矢田川の鯉　さん2008/11/3　1:20魚類です　
２９やぶコウノトリ　さん2008/11/4　13:38兵庫県　
３０ゴンとも　さん2008/11/3　16:01豊川市　
３１タカピー　さん2008/11/3　21:58中学生　
３２巷の夢　さん2008/11/4　7:17宮城県出身　
３３ＫＡＺ　さん2008/11/4　9:43熊本県　
３４魔法使いサリン　さん2008/11/4　15:02滋賀県　
３５元気モリモリ　さん2008/11/4　20:20宮崎県　
３６川上智弘　さん2008/11/5　0:10兵庫県　
３７ ゆうり　さん2008/11/6　16:01作曲家　
３８川村高雅　さん2008/11/6　16:53神奈川県　
３９理科ちゃんマン　さん2008/11/6　21:58理科の塾講師＠兵庫県
４０SaiSai　さん2008/11/7　11:36大阪市・走るプログラマ
４１阿修羅　さん2008/11/7　12:31長野県小学校教諭
４２す　さん2008/11/7　15:38城崎　
４３masaK　さん2008/11/7　15:38兵庫県香美町出身
４４kasama　さん2008/11/12　15:09和歌山県プログラマ
４５ぴーしゅん　さん2008/11/21　15:21　
４６中3(復活)!?航空アニマル　さん2008/11/21　19:58東京都26市内中学3年生
４７がんばれ山手線　さん2008/11/23　22:37横浜市
４８ぱん　さん2008/11/28　9:55　
４９よっち　さん2008/11/30　17:31栃木県

　
[128] 中央で分割されない通りを先に 投稿者：す 投稿日：2008/11/07(Fri) 15:48 [返信]

[122]と同様に考えました。
1)中央で分割されない組み合わせは、例と上下逆さにした
　2通りしかない。
2)中央で分割される場合、片方側で3通りある
3)よって、3×3＋2＝11（通り）

8畳とか12畳だとどうなるのだろう。
なんか法則があるかもしれませんね。
追求すれば面白い問題かもしれません。

　
[127] もれなく数えるしか・・？ 投稿者：安楽 投稿日：2008/11/07(Fri) 14:41 [返信]

図形ソフトを使って、あれこれ考えて楽しめました。

　
[126] 11通りですね！ 投稿者：理科ちゃんマン 投稿日：2008/11/06(Thu) 21:55 [返信]

理科の塾講師＠兵庫県

　
[125] 無題 投稿者：ゆうり 投稿日：2008/11/06(Thu) 16:03 [返信]

私も対称性を利用して、数え上げました。

　
[124] 無題 投稿者：鞍馬の天狗 投稿日：2008/11/03(Mon) 19:15 [返信]

有名な問題です
小学校時代
６畳の広い方がいい（11）
と覚えました

　
[123] 無題 投稿者：fisherman 投稿日：2008/11/01(Sat) 21:03 [返信]

とにかく，数えました。

　
[122] 場合分けするとしたら・・ 投稿者：Mr.ダンディ 投稿日：2008/11/01(Sat) 00:53 [返信]

[左端に縦長の畳があり、その右に横長の畳が接している場合]・・縦長が上辺にも接するか、下辺に接するかの２種類
（この場合、長方形が縦の直線で分割されていない）

[上記２種類以外]長方形が中央を通る直線により、左右に分割される。
縦×横＝3×2 の長方形の敷き詰め方は３通りあるから、3×3＝9（通り）
よって、２＋９＝１１（通り）

ただし、この広さではあれこれ考えずに、すべてもれなく数え上げたほうが早いかも。