「今月の問題」　第１１２回　（平成２１年１月）


＜問題＞

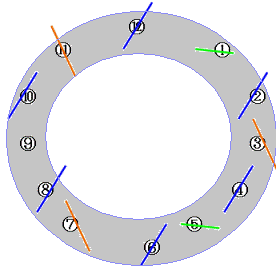
　左図を見てください。時計回りに@からKまで番号のついた回転寿司のネタが回っています。Aが書かれた寿司ネタから始めて１枚おきに寿司ネタを取っていき、最後の１枚になるまで続けていきます。
　つまり、取り除かれる順はACEGIKBFJD@で最後に残った寿司ネタはHになります。

　ここで問題です。もし、１〜192まで書かれた192枚の寿司ネタを、２から１枚おきに取り続けていくと、最後に残るのは何番の寿司ネタでしょうか。

＜ミニ知識　　回転寿司＞

　回転寿司は大阪の立ち喰い寿司店経営者が、ビール製造のベルトコンベアをヒントに、多数の客の注文を低コストで効率的にさばくことを目的として「コンベヤ旋廻食事台」を考案したことが始まりだそうです。
　その店は、私の生まれた1958年に、大阪府東大阪市の近鉄布施駅北口に開かれた「元禄寿司」が第１号店だそうです。
　コンベアは、ほぼ100%が石川県で製造されているようですが、皿を載せたチェーンコンベアは時計回りに回るのが多いのは、箸を持った右利きの人が取りやすいようにとの配慮によるものだそうです。

←回転寿司の元祖・元禄寿司本店

＜正解者一覧表＞　 　　　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１NAMPOTのPOT さん2009/1/1　0:09　
　２algebra さん2009/1/1　0:13神奈川県
　３teki さん2009/1/1　0:15大阪府
　４Ｍｒ.ダンディ さん2009/1/1　0:23大阪府
　５ゴンとも さん2009/1/1　0:27　
　６ma-mu-ta さん2009/1/1　1:07東京都　
　７信三 さん2009/1/1　3:47ゴールデンゲイトパークの隠居
　８oguchan1 さん2009/1/1　4:10鹿児島県　
　９いちもく さん2009/1/1　4:21立川市　
１０スモークマン さん2009/1/1　6:17朝まで観ちゃいました...^^;v
１１akira さん2009/1/1　7:30東京都　
１２uchinyan さん2009/1/1　9:12東京都　
１３GEN さん2009/1/1　11:27長野　
１４ラスカマン さん2009/1/1　11:31静岡県伊豆半島
１５S田 さん2009/1/1　12:51　
１６なにわ さん2009/1/1　13:17西宮市　
１７経友会の進作 さん2009/1/1　13:41京都府木津川市・７０歳
１８りーくん さん2009/1/1　14:04埼玉県　
１９ゆうり さん2009/1/1　16:04神奈川県　作曲家
２０fisherman さん2009/1/1　18:31豊岡市・塾講師
２１マッキー２７ さん2009/1/1　19:27愛知県
２２nak さん2009/1/2　13:51鹿児島県　
２３タカピー さん2009/1/2　16:42中学生　
２４ルルゥ さん2009/1/2　18:23　
２５数学爺 さん2009/1/3　16:54神奈川県　
２６理科ちゃんマン さん2009/1/3　18:18理科の塾講師＠兵庫県
２７川上智弘 さん2009/1/4　17:17兵庫県
２８ひろ さん2009/1/4　21:33徳島県
２９航空アニマル さん2009/1/5　1:45東京都26市内中学3年生
３０巷の夢 さん2009/1/5　7:42宮城県出身
３１かず さん2009/1/5　10:56熊本県
３２あすかｓ さん2009/1/5　13:25　
３３やぶコウノトリ さん2009/1/5　15:01兵庫県養父市　
３４元気モリモリ さん2009/1/6　17:11宮崎県　
３５ まいすた　さん2009/1/6　22:08　
３６ぴーしゅん さん2009/1/7　10:07　
３７SaiSai さん2009/1/7　10:12大阪市　
３８ kasama さん2009/1/7　11:24和歌山県プログラマー
３９安楽 さん2009/1/7　16:33宮崎県　
４０す さん2009/1/8　21:11城崎　
４１きらら さん2009/1/9　9:29新潟県　
４２新俳人澄朝 さん2009/1/10　12:37津山市　
４３矢田川の鯉 さん2009/1/21　15:54魚類です　
４４tomo2 さん2009/1/22　15:51東京都　
４５男はつらいよ さん2009/1/27　11:43神奈川県　

　
[145] 謹賀新年 投稿者：ゆうり 投稿日：2009/01/01(Thu) 16:03 [返信]

横一列に並べて考え、
それぞれの周回が偶数か奇数で場合分けをして答えを出しました。
　
[143] 謹賀新年 投稿者：スモークマン 投稿日：2009/01/01(Thu) 06:13 [返信]

本年もよろしくお願い申し上げます m(_ _)mγ

2^8,2^16 の時のアナロジーで推測 ^^; Orz...
2^k のとき、1が残り、2^k+1 のとき、3 が残り、・・・
192=2^7+64　なので、
1+2*64=129
♪

　
[141] 一般式は 投稿者：ゴンとも 投稿日：2009/01/01(Thu) 00:59 [返信]

J(2^m+l)=2*l+1　でこの場合は
J(192)=J(2^7+64)=2*64+1=129・・・・・・(答え)

　
[140] 明けましておめでとう御座います 投稿者：Mr.ダンディ 投稿日：2009/01/01(Thu) 00:42 [返信]

残る数の形が順に
2ｎ＋1, 4ｎ＋1, 8ｎ＋1, 16ｎ＋1, 32ｎ＋1, 64ｎ＋1 ,128ｎ＋1　（ｎ：整数）
となって 1と129 が残った後、１が消えて129 が最後に残りました。
（途中で１を残すのかと思ったが、最後にならないようには工夫されていましたね）

皆さん本年もよろしくお願いいたします。