※問題が簡単すぎるという意見を頂きましたので、展開図を削除しました。ただし、この立体の正5角形の数は12、正6角形の数は20あることは分かっていることとします。(4/13)
<問題>
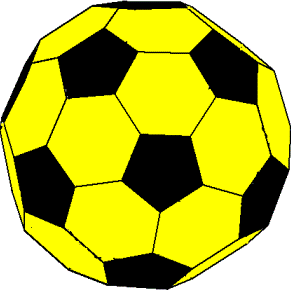
左図を見てください。正五角形と正六角形の多面体を組み合わせてサッカーボールを作りました。下図がその展開図です。
それぞれ五角形の周りは六角形に囲まれており、六角形の周りは五角形と六角形に交互に囲まれています。
る。
ここで問題です。サッカーボールの頂点の数(角の数)はいくらいくらになるでしょうか。
<ミニ知識 オイラーの多面体定理>
面が1種類の正多角形から構成される正多面体は5種類あることはよく知られています。
面が2種類以上の正多角形でかこまれて、しかも、球に内接することができる多面
体を準正多面体(または半多面体)といいますが人によって定義がいろいろあるようです。
いずれにしても、オイラーの多面体の定理によれば、面、頂点、辺の数の関係に「面の数
+ 頂点の数 = 辺の数 + 2」の関係があります。