「今月の問題」　第１１６回　（平成２１年５月）


※全国学力調査問題に近づけるために、箱の中の当たりが入っている数を３つに変更します。ご了解下さい。（5/1　6:00）

＜問題＞

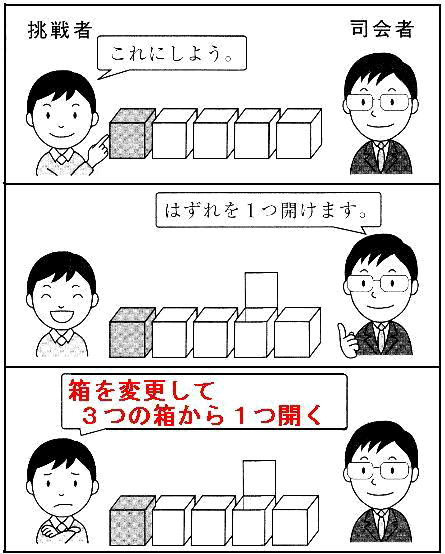
　挑戦者の前に５つの箱が置かれています。その５つの箱の中で３つには、賞品が入っている当たりの箱です。司会者はどれが当たりの箱か知っています。
　次のようにゲームを進めました。
@　挑戦者は、最初に１つの箱を選びますが、中を見ることができません。
A　司会者は、残った４つの箱のうち、はずれの箱を１つ開けて見せます。
B　挑戦者は、最初に選んだ箱を変更し、開いていない３つの箱の１つを選択して開きます。

　ここで問題です。@からBの操作をするとき、挑戦者が当たりを選ぶ確率を求めてください。
　　　　　（※答えは分数で答えてください）

　

＜ミニ知識　　全国学力学習状況調査2009＞

 　この問題は平成21年全国学力学習状況調査問題　中学３年数学Ｂの問題を少しだけ発展させたものです。
　Ｂ問題は、知識・技能問題を活用する力を見ることを目的に作られています。
　授業では扱わないような問題も出題されています。数学の力以上に、問題文を読み取り理解する力が必要とされるように思います。

＜正解者一覧表＞　 　　　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１Ｍｒ.ダンディ さん2009/5/1　0:09大阪府　
　２algebra さん2009/5/1　0:23神奈川県　
　３数学 さん2009/5/1　0:34　
　４経友会の進作　さん2009/5/1　0:48京都府木津川市・７０歳
　５男はつらいよ さん2009/5/1　1:12神奈川県　
　６ゴンとも　さん2009/5/1　2:32豊川市　
　７信三 さん2009/5/1　3:45ゴールデンゲイトパークの隠居
　８いちもく さん2009/5/1　5:25立川市　
　９次郎長 さん2009/5/1　8:02兵庫県　
１０uchinyan さん2009/5/1　8:36東京都　
１１やぶコウノトリ さん2009/5/1　10:17兵庫県　
１２９期生 さん2009/5/1　12:30初芝立命館中学校
１３元気モリモリ さん2009/5/1　12:36宮崎県　
１４りーくん さん2009/5/1　14:43埼玉県　
１５fisherman さん2009/5/1　16:44豊岡市・塾講師　
１６新俳人澄朝　さん2009/5/1　18:33津山市　
１７tomo2　さん2009/5/1　20:54東京都　
１８nak　さん2009/5/1　22:04鹿児島県　
１９ まいすた　さん2008/5/1　22:32　
２０ラスカマン　さん2009/5/1　22:48静岡県伊豆半島　
２１teki　さん2009/5/1　22:58大阪府　
２２マッキー２７　さん2009/5/2　0:04愛知県　
２３ガウス　さん2009/5/2　0:34福岡県　
２４wowka　さん2009/5/2　7:39静岡県　
２５宮崎隆行　さん2009/5/2　14:34　
２６pao　さん2009/5/2　18:03　
２７ma-mu-ta　さん2009/5/3　0:07東京都　
２８スモークマン　さん2009/5/3　12:33目指せ囲碁５段！
２９六角三つ　さん2009/5/3　22:12滋賀県　
３０kasama　さん2009/5/4　12:28和歌山県プログラマ
３１アーコ　さん2009/5/4　17:10インド
３２ゆうり　さん2009/5/4　19:48神奈川県　作曲家
３３y.okada　さん2009/5/4　20:58　
３４ tx2005　さん2009/5/5　13:53茨城県　
３５反車　さん2009/5/6　20:58大阪　
３６鯨鯢(Keigei)　さん2009/5/6　8:40太平洋　
３７マグロ皇帝　さん2009/5/6　12:45茨城県south park
３８oguchan1　さん2009/5/6　16:46鹿児島県　
３９ひろたん　さん2009/5/6　22:26埼玉県　
４０ルルゥ　さん2009/5/7　1:27新潟市　
４１川上智弘　さん2009/5/7　20:12兵庫県　
４２す　さん2009/5/10　13:37城崎　
４３巷の夢　さん2009/5/11　6:45宮城県出身　
４４ＫＡＺ　さん2009/5/11　19:45熊本県　
４５理科ちゃんマン　さん2009/5/16　23:27理科の塾講師＠兵庫県
４６codra　さん2009/5/17　17:06愛知県
４７嵐山と結城美柑はラヴラヴvさん2009/5/18　21:44東京都
４８なにわ　さん2009/5/23　16:18西宮市
４９j8e2q6　さん2009/5/23　16:45　
５０肥満児　さん2009/5/30　22:15　

答えは、４／５　でした。
　
[215] 余事象で、、 投稿者：肥満児 投稿日：2009/05/30(Sat) 22:15 [返信]

はずれる確率は(3／5)*(1／3)=1／5　　　　　　　　　　　　　　　　　　　　　　よって1-1／5=4／5

　
[214] 199の方ありがとうございました 投稿者：tx2005 投稿日：2009/05/15(Fri) 08:16 [返信]

>>199
お返事が遅くなり誠に申し訳ありませんでした。なるほど、そのような考え方もあるのですね。参考になりました。ありがとうございました。

　
[213] とりあえず・・・ 投稿者：una 投稿日：2009/05/12(Tue) 20:38 [返信]

式はこうなりました。
2/5*1+3/5*2/3=2/5+2/5=4/5=80％

とりあえずやってみましたが、みなさんレベルが高いです＾＾；

　
[212] こんな求め方は？ 投稿者：田中 投稿日：2009/05/11(Mon) 19:54 [返信]

@１番目に選んだものが当たりだったとすると、2回目は変更しなければならないので、残りの３つの中から２つが当たりになる。よって、2/3。これが6通りあるから、2/3*6=4…ア
A１番目に選んだものがはずれである場合は、変更後、必ず当たりが出る。よって、確率は１。これは4通りあるから、1*4=4…イ
B全部で選び方は10通りあるので、@、Aより、(ア+イ)/10=4/5

　
[211] やはり 4/5 です 投稿者：鯨鯢(Keigei) 投稿日：2009/05/09(Sat) 09:20 [返信]

普通に考えれば、挑戦者が最初にはずれを選ぶ場合と当たりを選ぶ場合で、
(2/5)*(3/3)+(3/5)*(2/3)=2/5+2/5=4/5 ですね。
数字が書かれている部分の流し読みですが、皆さんのログを拝見していて、
次のような考え方が浮かびました。
はずれの箱を知っている司会者があらかじめ開ける箱を決めておいて、
司会者がその箱を開ける場合と挑戦者が先にその箱を選ぶ場合で、
(4/5)*(3/4)+(1/5)*(3/3)=3/5+1/5=4/5 となります。
なお、「実験」は[204]の30通りが均等にあらわれると思います。


　
[210] Re:[208] 実験してみました 投稿者：uchinyan 投稿日：2009/05/08(Fri) 18:24 [返信]

> > 今回の問題では，最初の箱を除いた四つの箱からハズレを一つ見せるのだから，最初の箱はいわば隔離されており，
> > この操作に関与しておらず，最初の箱の確率が変わる原因にはならないと思います。
>
> なるほど。
> この意見が今までの中で一番質問に対する答えに近いと思います。理由が見えます。
> 選んだ物を隔離するという仮定で話をすすめて結論出したあとの仮定の根拠や説明もスッキリできそう。
> 同じ方向性の意見はありましたがより明快な書き方をされていると思います。
取り敢えず，言いたいことが伝わったようで，よかったです ^^/

　
[209] Re:[206] 実験してみました 投稿者：Mr.ダンディ 投稿日：2009/05/08(Fri) 18:10 [返信]

私の表現力では同じ説明の繰り返ししかでできないなと思っているところ、uchinyan
さんの書き込みがありましたので、違った説明ならどうなるのか静観させていただきました。

なるほど、uchinyanさんのように
> 最初の箱はいわば隔離されており、この操作に関与しておらず，最初の箱の確率が変わる原因にはならない。
と説明したほうが説得力
がありますね。

Wikipedia流や私の(解法1)は正しいと思っていますが、確かに「なにか狐につままれた
ような？」と思う人と、「なるほど！」と思う人に分かれるような解法だとは思います。

前述のつたない説明、失礼致しました。

　
[208] Re:[206] 実験してみました 投稿者：tomo2 投稿日：2009/05/08(Fri) 14:55 [返信]

> 今回の問題では，最初の箱を除いた四つの箱からハズレを一つ見せるのだから，最初の箱はいわば隔離されており，
> この操作に関与しておらず，最初の箱の確率が変わる原因にはならないと思います。

なるほど。
この意見が今までの中で一番質問に対する答えに近いと思います。理由が見えます。
選んだ物を隔離するという仮定で話をすすめて結論出したあとの仮定の根拠や説明もスッキリできそう。
同じ方向性の意見はありましたがより明快な書き方をされていると思います。
ありがとうございます。

> 実験の結果としての数値が違っていれば，まずは，考え方，仮説ですね，を疑うのは，実証科学の基本です。

計算で数値が違ってるからこそ理由や考え方の話を求めていたのです。[201]に書いた通りです。
他の解法使っても数値は出ます。
ゆえにわかっている数値を求める実験をすることはこの件には繋がりません。

言った言わないあなたの見解は云々とかそういうことはどうでもいいのです。
「このように考える、なぜなら〜」という根拠がいただきたかった、ということです。

　
[207] ちょっと追加　Re:[206] 実験してみました 投稿者：uchinyan 投稿日：2009/05/08(Fri) 13:30 [返信]

個人的には，Wikipedia流や[182]の Mr.ダンディさんの(解法1)は，直感的ですが，誤解を招きやすい気がしています。
数学的には，あやふやな感じ(あくまでも感じです。)もします。

[182]の(解法2)の方が，考えやすいと思います。

　
[206] Re:[205] 実験してみました 投稿者：uchinyan 投稿日：2009/05/08(Fri) 11:14 [返信]

> > しかし，そうした最初の箱に関わる操作を行わないで確率が 3/5 -> 3/4 に突如変わると考えるのは理解できません。
>
> 確率が変動しないことは当然という前提の上で考えているからでしょう。
> 変動しない理由を説いていただきたかったことが今回の件です。
> それに対し、このケースは変動しないのが当たり前
> という回答があってもそれは理由にはならないと思いますよ。
誰も確率が変わらないなどとは言っていませんよ。
実際，最初の箱を残り三つの箱と一緒にして四つの箱から一つ選ぶ場合は，3/5 -> 3/4 に変わる，と言っています。
確率が変わるのにはその対象に関わる何らかのきっかけ，原因，があり，その結果として変わるのだ，という主張です。
tomo2さんが，確率が変わる理由を(明確に)示していない，少なくとも私はそう思います，と言っているのです。

今回の問題では，最初の箱を除いた四つの箱からハズレを一つ見せるのだから，最初の箱はいわば隔離されており，
この操作に関与しておらず，最初の箱の確率が変わる原因にはならないと思います。

ルールが変わって，五つの箱からハズレを一つ見せるのならば，最初の箱が開けられる可能性もあるわけで，
もし最初の箱が開けられなければ，最初の箱がハズレの可能性は確かに減り，確率は 3/5 -> 3/4 に変わります。

tomo2さんは，ここらを混乱なさっているように思います。

> 試すことを否定しませんが、数値の検証ならともかくとして
> 考え方やその理由の解明にどこまで有用なのか私にはわかりません。
実験の結果としての数値が違っていれば，まずは，考え方，仮説ですね，を疑うのは，実証科学の基本です。

[205] Re:[203] 実験してみました 投稿者：tomo2 投稿日：2009/05/08(Fri) 01:40 [返信]

> しかし，そうした最初の箱に関わる操作を行わないで確率が 3/5 -> 3/4 に突如変わると考えるのは理解できません。

確率が変動しないことは当然という前提の上で考えているからでしょう。
変動しない理由を説いていただきたかったことが今回の件です。
それに対し、このケースは変動しないのが当たり前
という回答があってもそれは理由にはならないと思いますよ。

試すことを否定しませんが、数値の検証ならともかくとして
考え方やその理由の解明にどこまで有用なのか私にはわかりません。

自分なりに噛み砕いて書いていたつもりではあるのですが
伝わらないということはきっと書き方が悪かったのですね。

　
[204] 4/5 です 投稿者：鯨鯢(Keigei) 投稿日：2009/05/07(Thu) 22:35 [返信]

箱1,2がはずれで、3,4,5が当たりとします。
30回の試行での割合を考えると、挑戦者がそれぞれの箱を選ぶのは6回ずつ。
123,123,124,124,125,125 ← 挑戦者が1を選ぶと司会者は2、挑戦者は同率で3,4,5を選ぶ
213,213,214,214,215,215 ← 挑戦者が2を選ぶと司会者は1、挑戦者は同率で3,4,5を選ぶ
312,314,315,321,324,325 ← 挑戦者が3を選ぶと司会者は同率で1,2、挑戦者は同率で残りを選ぶ
412,413,415,421,423,425 ← 挑戦者が4を選ぶと司会者は同率で1,2、挑戦者は同率で残りを選ぶ
512,513,514,521,523,524 ← 挑戦者が5を選ぶと司会者は同率で1,2、挑戦者は同率で残りを選ぶ
この30個の中に最終的なはずれが6回、当たりが24回、当たる確率は24/30=4/5
ということで、他に特別な条件がない限り4/5ですよね。


　
[203] Re:[201] 実験してみました 投稿者：uchinyan 投稿日：2009/05/07(Thu) 12:52 [返信]

えと，数学も実証科学の一翼を担う以上，実際に試してみることは重要だと思います。

私個人としては．．．
tomo2さんは，最初に選んだ箱の確率が変わらないことに疑問をもたれているようですが，
私はむしろ反対に，その後は最初の箱に関わらない操作を行っているのに，
tomo2さんが最初の箱の確率が変わると思われていることが不思議でしょうがないです。

もちろん，四つの箱からハズレを見せた後で，残りの箱と最初の箱を一緒にして再度選び直し，
それが最初の箱と同じだった場合の当たりの確率は 3/4 でしょう。
しかし，そうした最初の箱に関わる操作を行わないで確率が 3/5 -> 3/4 に突如変わると考えるのは理解できません。

ちなみに，今回の問題の，Wikipedia流 又は Mr.ダンディさんの(解法1) では，
(四つの箱ではなく)三つの箱から選ぶ際に，浮いた 3/5 が三つの箱に等分配され，
3/5 -> 3/5 + 3/5 * 1/3 = 4/5 になるのだと理解しています。
なお，四つの箱から選ぶのならば，3/5 が四つの箱に等分配され，3/5 -> 3/5 + 3/5 * 1/4 = 15/20 = 3/4 です。

　
[202] Re:[195] Re:これは 投稿者：tomo2 投稿日：2009/05/06(Wed) 17:52 [返信]

[201]の書き込みを踏まえた上での返信です。

> 開けた結果がたまたまハズレであるならそうですが、司会者がハズレを意図的に開
> けており、挑戦者もそれを知っているのでその考えはおかしいです。

この論で見渡すには「司会者が情報を持っていることで確率が持ち越される」
という点を解明しないと繋がってきません。

>> 初めに何を選ぼうと、他にハズレがあることは初めから分かっており、その１つを
>> あけようと選んだものの当たりやすさが大きくなるわけはありません。

以前挙げられていた上記意見のなぜなら部分があればスッキリすると思います。

> はじめに選んだ箱と、意図的に残された３つの箱とは同じように考えてはいけないで
> すね。４つは意図的に操作を加えられた時点で２種類の確率を持ったものに分かれ
> ています。

情報により条件分岐するという認識であってるみたいですね。

> 逆に訊きますが、初めに何を選ぼうと、他にハズレがあることは初めから分かって
> おり、その１つが開けられたところでどうして当たりやすさが変わるのでしょうか。

「司会者が情報を持っている〜」という件と直結しているので、
そこが見えないと「4つのうちから3つ選ぶ」との説明をしてループになります。

> ２人の判断が分かれるのは無理のないのところですが、実際に与えられた条件の１部
> しか知らない者の判断を尊重するということは、抜かした条件に目をつぶりなさいと
> いうことと同じです。

ということは、
問題の算出をしようとしているポイントや視点が違うとそれらの情報のせいで
条件が変わってしまう、つまり文章をどう解釈するかが大切になるのですね。
これは文章中の事柄を明確にすることで解決しそうですね。

　
[201] Re:[196] 実験してみました 投稿者：tomo2 投稿日：2009/05/06(Wed) 17:35 [返信]

> 十進ベーシックのプログラムでシミュレートしてみました。

検算ありがとうございます。
これは当然の結果だと思います。

どの数値が正しいということを論点としたいわけではありません。
どう考えるとこうになるという話が聞きたかったのです。
問題を解く過程での疑問を紐解いていけば
一般的と言われる範囲ではどのように考えるかの方向性がみえ、
その理由はどこにあるなどわかると思ったのです。
問題の解釈で差がうまれるのなら文章の読み方でおきるのか
文章の書き方や問い方でおきているのか、そういったところが気になります。

〜は〜である。という公式や思い込みの部分ではなく、
その先の「なぜなら〜だからである」というところを理解したいのです。
答えが出るからそれでいいでは思考停止になってしまい危険だと思ってます。

今回の問題で私的に考え方が分岐する場所があるので別視点から取り上げました。
ですので3/5となる理由を問いかけたというわけです。

　
[200] 普通に 投稿者：マグロ皇帝 投稿日：2009/05/06(Wed) 12:43 [返信]

普通にといってもぼくの低い学力での普通ですので、

ぼくはとりあえず、最後に当たる確立ということで、最初にはずれを選んだ場合は必ず当たるということに気づいた、というだけで後はｔｘさんと一緒の方法でした。

しかし、シュミレーションとは・・・・
凄すぎですね


　
[199] Re:[198] 普通に（？）考えてみました 投稿者：Mr.ダンディ 投稿日：2009/05/06(Wed) 09:08 [返信]

> 場合分けしないで求める方法はないのでしょうか・・・？
[180][181]での私の[解法１][解法3]、および[189]で書かれてあるwikipediaの解説
などはどうでしょう。

> uchinyanさん
プログラムによる実験結果　有難うございます。（確率において、シミュレーション
は妙に説得力があるものですね・・論より証拠？）

　
[198] 普通に（？）考えてみました 投稿者：tx2005 投稿日：2009/05/05(Tue) 13:57 [返信]

最初に選択したものが当たりかはずれかで場合分けをして、

（１）当たりだった場合（の最終的に当たりを選択する確率）
３／５×３／２＝２／５
（２）はずれだった場合（の最終的に当たりを選択する確率）
２／５×３／３＝２／５

よって２／５＋２／５＝４／５となりました。

場合分けしないで求める方法はないのでしょうか・・・？

　
[197] プログラム　Re:[196] 実験してみました 投稿者：uchinyan 投稿日：2009/05/05(Tue) 11:00 [返信]

> 十進ベーシックのプログラムでシミュレートしてみました。
> プログラムは別に示しますが，
プログラムです。冗長なので，追いやすいと思います (^^;

RANDOMIZE

DIM box(5), index1(4), index2(3)
LET m = 1000000

FOR n = 1 TO m

　IF MOD(n,10000) = 0 THEN
　　PRINT "試行回数："; n; "回"
　END IF

　REM 当たり及びハズレを設定
　FOR i = 1 TO 5
　　LET box(i) = 1
　NEXT i
　LET lose1 = INT(RND * 5) + 1
　DO
　　LET lose2 = INT(RND * 5) + 1
　LOOP WHILE (lose2 = lose1)
　LET box(lose1) = 0
　LET box(lose2) = 0

　REM 今回の問題の場合

　REM 最初に五つの箱から一つ選ぶ
　LET choice1 = INT(RND * 5) + 1

　REM 残りの四つの箱から一つハズレを見せる
　LET i = 0
　FOR j = 1 TO 5
　　IF j <> choice1 THEN
　　　LET i = i + 1
　　　LET index1(i) = j
　　END IF
　NEXT j
　IF choice1 <> lose1 THEN
　　LET lose = lose1
　ELSE
　　LET lose = lose2
　END IF

　REM 残りの三つの箱から一つ選ぶ
　LET i = 0
　FOR j = 1 TO 4
　　IF index1(j) <> lose THEN
　　　LET i = i + 1
　　　LET index2(i) = index1(j)
　　END IF
　NEXT j
　LET choice2 = INT(RND * 3) + 1

　REM 一番目に選んだ箱が当たり
　LET win1Count1 = win1Count1 + box(choice1)

　REM 二番目に選んだ箱が当たり
　LET win1Count2 = win1Count2 + box(index2(choice2))

　REM 確率を表示
　IF MOD(n,10000) = 0 THEN
　　PRINT "・今回の問題の場合"
　　PRINT "　一番目に選んだ箱が当たり："; win1Count1/n
　　PRINT "　二番目に選んだ箱が当たり："; win1Count2/n
　END IF

　REM 先に五つの箱からハズレを見せる場合

　REM 五つの箱から一つハズレを見せる
　REM 見せるハズレは lose1 とする

　REM 残り四つの箱から一つを選ぶ
　LET i = 0
　FOR j = 1 TO 5
　　IF j <> lose1 THEN
　　　LET i = i + 1
　　　LET index1(i) = j
　　END IF
　NEXT j
　LET choice1 = INT(RND * 4) + 1

　REM 残り三つの箱から一つを選ぶ
　LET i = 0
　FOR j = 1 TO 4
　　IF j <> choice1 THEN
　　　LET i = i + 1
　　　LET index2(i) = index1(j)
　　END IF
　NEXT j
　LET choice2 = INT(RND * 3) + 1

　REM 一番目に選んだ箱が当たり
　LET win2Count1 = win2Count1 + box(index1(choice1))

　REM 二番目に選んだ箱が当たり
　LET win2Count2 = win2Count2 + box(index2(choice2))

　REM 確率を表示
　IF MOD(n,10000) = 0 THEN
　　PRINT "・先に五つの箱からハズレを見せる場合"
　　PRINT "　一番目に選んだ箱が当たり："; win2Count1/n
　　PRINT "　二番目に選んだ箱が当たり："; win2Count2/n
　　PRINT
　END IF

NEXT n

END


　
[196] 実験してみました 投稿者：uchinyan 投稿日：2009/05/05(Tue) 10:50 [返信]

十進ベーシックのプログラムでシミュレートしてみました。
プログラムは別に示しますが，100万回の試行で，

試行回数： 1000000 回
・今回の問題の場合
　一番目に選んだ箱が当たり： .600077
　二番目に選んだ箱が当たり： .800158
・先に五つの箱からハズレを見せる場合
　一番目に選んだ箱が当たり： .749989
　二番目に選んだ箱が当たり： .74942

となりました。やはり

・今回の問題の場合
　一番目に選んだ箱が当たり： 3/5
　二番目に選んだ箱が当たり： 4/5
・先に五つの箱からハズレを見せる場合
　一番目に選んだ箱が当たり： 3/4
　二番目に選んだ箱が当たり： 3/4

となるのが妥当だと思います。

ご参考まで。

　
　
[195] Re:[193] Re:これは 投稿者：Mr.ダンディ 投稿日：2009/05/04(Mon) 23:48 [返信]

> 司会者がはずれを知っていてもいなくても1つ開封し、
> それがはずれであったという事実でしかないはず。
開けた結果がたまたまハズレであるならそうですが、司会者がハズレを意図的に開
けており、挑戦者もそれを知っているのでその考えはおかしいです。

> 未開封箱4つ中に3つ当たりがある(3/4)にもかかわらず3/5であると。
はじめに選んだ箱と、意図的に残された３つの箱とは同じように考えてはいけないで
すね。４つは意図的に操作を加えられた時点で２種類の確率を持ったものに分かれ
ています。

> しかし未開封箱が4つになっても選んだ箱が3/5であり続ける理由は
> 選んだときは未開封箱が5つあったくらいしか見えてこない
逆に訊きますが、初めに何を選ぼうと、他にハズレがあることは初めから分かって
おり、その１つが開けられたところでどうして当たりやすさが変わるのでしょうか。

> > 挑戦者A,挑戦者Bの話ですが、Ｂの持っている情報がＡの持つ情報の一部である場合は
> > 、Ａの持っている情報に基づいた結論が優先されますね。
> なぜ優先されるのですか？
２人の判断が分かれるのは無理のないのところですが、実際に与えられた条件の１部
しか知らない者の判断を尊重するということは、抜かした条件に目をつぶりなさいと
いうことと同じです。
（本題では司会者の操作を知らないものの判断を尊重することは司会者の操作に目
をつぶることになります）

　
[194] Re:[193] Re:これは 投稿者：tomo2 投稿日：2009/05/03(Sun) 17:50 [返信]

> （開けたところでハズレが残っていることを確認したに過ぎません）

多分ここの見解でわかれているのだと思います。
箱が5つあって当たりが3つはずれ2つそのうちのはずれ1つが見えている
ということは未開封の箱を考えると
箱が4つあって当たりが3つはずれ1つになります。
期待値の和を計算するなら(3/4)*4=3になります。

未開封箱5の時に1つ選ぶと3/5で間違いないでしょう。
次に司会者が1つ開封してはずれをみせていますが、挑戦者からすると
司会者がはずれを知っていてもいなくても1つ開封し、
それがはずれであったという事実でしかないはず。
そうなると未開封箱が4つあり当たりが3つ、
選んだ箱は未開封箱4つ中の1つである。
ただ選んだときは未開封箱5のときであった、となります。
選んだときは3/5であるのは確か。
しかし未開封箱が4つになっても選んだ箱が3/5であり続ける理由は
選んだときは未開封箱が5つあったくらいしか見えてこない。
未開封箱4つ中に3つ当たりがある(3/4)にもかかわらず3/5であると。

答えが見えてしまっている箱を考慮する理由があれば変わるのかも。


> 挑戦者A,挑戦者Bの話ですが、Ｂの持っている情報がＡの持つ情報の一部である場合は
> 、Ａの持っている情報に基づいた結論が優先されますね。

なぜ優先されるのですか？
ここの理由がわかればスッキリしそうです。

5本のクジはAさんBさんともに妥当です。
Aさんは5つの中に2つの当たりでa-cに1つd-eに1つ当たりがあること知っており、
bはa-cの中に該当、つまり3つ中1つ当たるから1/3。
Bさんはa-eの5つの中に2つ当たりがあるから2/5になります。
Bさんから見ればAさんの答えはおかしいはずです。
AさんがBさんに説明するにあたりなぜならの部分が前提の情報にあります。
つまり過程の情報により条件分岐してます。
条件が変われば答えが変わりますので両方妥当です。

　
[193] [192] Re:[190] これは 投稿者：Mr.ダンディ 投稿日：2009/05/03(Sun) 13:00 [返信]

初めに何を選ぼうと、他にハズレがあることは初めから分かっており、その１つを
あけようと選んだものの当たりやすさが大きくなるわけはありません。
ハズレが残っていることなど初めから見越したことです。
（開けたところでハズレが残っていることを確認したに過ぎません）

また、選んだものが途中で3/4になるのなら、どれを選んでも必ず同じことが起こる
ので 期待値の和が　(3/4)×5＞3　となってしまいます。

挑戦者A,挑戦者Bの話ですが、Ｂの持っている情報がＡの持つ情報の一部である場合は
、Ａの持っている情報に基づいた結論が優先されますね。

例えば、ａ,ｂ,ｃ,ｄ,ｅの５本のクジがあり
Ａさんには、(1)５つの中に２つ当たりがあります。(2) ｄ,ｅのうちでは１つが当たりです。
の２つの確かな情報を知らせ
Ｂさんには (1)の情報のみを知らせます。
今Ａさんに「ｂがあたりである確率は？」と訊いた後、あとからきたＢさんにも
同じ質問をしたとき、実際の確率としてはＡさんが答える1/3 とＢさんが答える 2/5
　のどちらが妥当かでしょうか？　あきらかですね。

以上のように考えます。

　
[192] Re:[190] これは 投稿者：tomo2 投稿日：2009/05/02(Sat) 19:47 [返信]

ご説明ありがとうございます。
(イ)と(ロ)の違いは司会者がはずれの情報を知っているか否かですよね。
情報を知っていると持ち越されるということでしょうか。
(ロ)について考えてみたのですが、
司会者がはずれを開けてみせたところで未開封箱の総数が4です。
結局4つ中に3つ当たりがあるということになると思います。
そうなると(イ)との違いがわかりません。

@の3/5の時点で選んだものだからA以降も適用されるということだろうとは思うのですが、
以下のような流れで考えてみます。
(@)挑戦者Aが@を行う
(A)司会者がAを行う
(B)挑戦者Aと@〜Aの過程を知らない挑戦者Bが挑戦者Aの選んだ箱の確率を求める
挑戦者Aの算出は3/5
挑戦者Bの算出は3/4
になると思います。
ここでポイントとしたいことは
挑戦者ABともに未開封箱4,開封箱(はずれ)1の中に3つ当たりがあるという時点で算出してることです。
事実として4個中に3個あるものに対しての算出なのにもかかわらず、
確率に差が出てしまっています。
数値の差は過程段階の情報の有無だと思います。
挑戦者Aは未開封箱5の時点で選択しているから3/5という主張になると思いますが、
確率を求めるところがはずれを1つ見せられた後で未開封4の時です。
となると当たり/総数の総数が減るのだから、
挑戦者Aが選択した箱は3/5の時点で選んだが、確率を求める時点では3/4になっているとも考えられると思います。

まとまりきれてない文章ですみません。
情報と確率変動の因果関係が明確ならばスッキリするのですかねぇ・・・。

　
[191] Re:[189] これは 投稿者：uchinyan 投稿日：2009/05/02(Sat) 16:51 [返信]

私も，Mr.ダンディさんのお考え，解釈，に賛成です。

なお，提示されているwikipediaの解説は，興味深く思いました。
Mr.ダンディさんの(解法1)に似ていますが，確率として 1 を超えないのがいいですね。
また，量子力学の観測の理論ぽくって面白いです。

　
[190] Re:[189] これは 投稿者：Mr.ダンディ 投稿日：2009/05/02(Sat) 09:09 [返信]

> @の時点で選択した箱の確率がA以降変わらない理由を知りたいです。

(イ) 司会者がどれがハズレかを知らずに無作為に選んだ「結果」がハズレであった場合は
、tomo2さんが書かれておられるように その時点で 3/4　になります。 ・・・が

(ロ)この問題の場合は、司会者が「外れ」を知っており、わざとハズレをあけています。
初めに何を選ぼうとも、ハズレが残っているのが分かっており、それを示したところ
で(初めに選んだものが当たっていそうかの)何の判断材料にもなりません。
だから 3/5が最後まで引き継がれることになります。

表現しにくかったのですが、私は以上のように捉えております。



　
[189] これは 投稿者：tomo2 投稿日：2009/05/01(Fri) 21:38 [返信]

モンティホール問題の類題ですよね。
以前からこの問題に非常に疑問を持っております。
wikipediaの解説にもずっと疑問を感じてました。

今月の問題の場合をwikipedia解説風に書くと、
@では箱すべてに3/5の確率があり、1つを選択。
Aで箱1つの5/3が→0になり、その確率が中に浮き、
Bでは@で選択した箱(3/5)以外の3つを選択するので
Aで中に浮いた3/5が3つの箱それぞれに分配(1/5づつ)
図の通り並べますと
@ 3/5 3/5 3/5 3/5 3/5
↓(はずれをみせる)
A 3/5 3/5 3/5 3/5→0 3/5
↓(はずれ分を3つに分配)
B 3/5 3/5+1/5 3/5+1/5 0 3/5+1/5

ということなのでしょうが、
@で選択した3/5が最後まで引き継がれる理由がわかりません。

私は以下の通り考えます。
@では5個中に3個入っているのだから3/5です。
Aでははずれを見せているので@の段階で選ぼうが、
はずれを見てから選ぼうが4個中に3個入っているので
答えを見せた箱以外の残り全ての箱は3/4です。
この時点で正解とされている答えからずれます。

@の時点で選択した箱の確率がA以降変わらない理由を知りたいです。
そもそもの考え方が間違ってる可能性も高いのでご教授いただけたら幸いです。

　
[188] 無題 投稿者：fisherman 投稿日：2009/05/01(Fri) 16:50 [返信]

2/5+2/5＝4/5に間違いないのに・・・？と何度もトライするも入れず。0．8でもダメ。なぜだ，ウ〜ン・・・。百分率なのか！

　
[187] Re:[186] うーむ　Re:計算し直しました 投稿者：uchinyan 投稿日：2009/05/01(Fri) 14:09 [返信]

なるほど。これならば，納得がいきますね。ある種，期待値のような。いわゆる期待値とは違いますが。

なお，箱が５つで当たりが４つの場合は，はずれの箱を開けない場合もあるので，微妙で，
ナイーブには，解法1ではうまくいかないように思いますが，
まぁ，これは特殊な場合と考えるのでしょうね。

ちなみに，解法2では，4/5 * 3/3 + 1/5 * 4/4 = 1 で，直感とも合います。

　
[186] [184] うーむ　Re:[182] 計算し直しました 投稿者：Mr.ダンディ 投稿日：2009/05/01(Fri) 13:21 [返信]

> Mr.ダンディさんのお考えを正確にたどれば，(3/5 * 4)÷3 = 4/5 でしょうか。
(3*4/5)÷3＝4/5 のところ　初め 12/5 としていたところ （3*4)/5 と修正し、
()は面倒なので省いたしだいです。

> ただ，3/5 * 4 が，気持ちは何となく分かるのですが，理由がいま一つピンときません。
確率を導入するとき、試験管に水がいっぱい入っているときの水の量を１としたとき、入っ
ている量がどれくらいかで確率はいくらかと表すという方法もありますね。

例えば５本の籤のうち２本当たりがある場合、隠していないときは、５本の試験管
のうち２本がいっぱいになっており それぞれが 0,1 がはっきりしているが、隠し
てしまうと、２本の水が５本に均等化され、どれもが 2/5ずつ入っている状態と考え
られ、１つずつのあたりの確率は　2/5 とする。
・・・というものです・・

本題の場合だと初め隠した段階で、すべての試験管に 3/5 水が入っている状態で、
初めに選んだもの以外の水の総量は、(3/5)*4＝12/5 と考え、そのうちの１本の水を
残り３本が均等になるよう分配にしたら、それら一本ずつに入っている量は
　12/5÷3＝4/5　ずつということになります。 → 確率 4/5

(要するに、確率を量と考え４本にあった確率(量)の和が３本に均等化されたとの考えでした。)


　
　
[185] 今回の問題の元ネタ 投稿者：ゴンとも 投稿日：2009/05/01(Fri) 12:01 [返信]

全国学力学習状況調査問題を

http://www.asahi.com/edu/chousa2009/

で見てみました。
たくさんの問題を45分で解くのは大変だと思いました。


　
[184] うーむ　Re:[182] 計算し直しました 投稿者：uchinyan 投稿日：2009/05/01(Fri) 11:09 [返信]

> 前記[解法1]によると・・・(3*4/5)÷3＝4/5
Mr.ダンディさんのお考えを正確にたどれば，(3/5 * 4)÷3 = 4/5 でしょうか。
ただ，3/5 * 4 が，気持ちは何となく分かるのですが，理由がいま一つピンときません。
そもそも，3/5 という確率の四つの和って何かな，と思うのですが，ナイーブにはやはり確率のような気がします。
しかし，3/5 * 4 = 12/5 > 1 なので，これはおかしいです。
そこらは，どう解釈なさっているのでしょうか。

ちなみに，私は，[解法2]で解きました。

　
[183] 場合分けしました。 投稿者：やぶコウノトリ 投稿日：2009/05/01(Fri) 10:16 [返信]

@であたりをとる場合　　3/5*2/3＝2/5
Aではずれをとる場合　　2/5*3/3＝2/5

　　　2/5+2/5＝4/5


　　

　
[182] 計算し直しました 投稿者：Mr.ダンディ 投稿日：2009/05/01(Fri) 08:30 [返信]

他の人の解法は？とここに入ろうとしたら入れず、よく見ると数値が変更されていましたので計算しなおしました。

前記[解法1]によると・・・(3*4/5)÷3＝4/5
前記[解法2]によると・・・(3/5)*(2/3)＋(2/5)*(3/3)＝4/5

「最初選んだ箱がはずれであった場合、必ず当たる」ことを考慮すると

[解法3] 外れる場合は「初めのものが当たり」かつ「2回目が外れている」場合に限られるから
外れる確率＝(3/5)*(1/3)＝1/5　・・・ 1−1/5＝4/5 が答え

よしおかさん、お褒め頂き有難うございます。かって類例で頭をひねったことがあり、そのときに[解法1]を考えつきました。

> そのためには、何より教師自身が、数学の面白さを感じなければなりません。
まさにその通りですね。「先生が数学を楽しみ、探究心を持ち続けている」これに勝るもの
は無いのではないでしょうか。いつまでも、その「みずみずしさ」でもって頑張ってください。

　
[181] 問題変更しました 投稿者：よしおか 投稿日：2009/05/01(Fri) 05:56 [返信]

いつも訪問ご参加ありがとうございます。
感謝、感謝、感謝です。
子ども達に、今、知識技能の活用する力と、関心意欲を持たせることが必要とされています。
そのためには、何より教師自身が、数学の面白さを感じなければなりません。
皆さんの、すばらしい回答のおかげで、何とか教師を続けていることができるような気がします。

さて、今回の問題は、4/21に行われた全国学力学習状況調査問題を利用しました。私は、今まで見たことがない問題で、なかなか問題の意味すら分かりませんでした。そこで、今月は、この問題にできるだけ近づける形で、当たりの数を３個にして、最初選んだ箱がはずれであった場合、必ず当たるという問題に変更しました。

PS：MRダンディさんの〔解法１〕すばらしいですね。このような考え方は、私には浮かんできません


　
[180] 面白い問題でした。 投稿者：Mr.ダンディ 投稿日：2009/05/01(Fri) 00:43 [返信]

[解法１]
初めは１つ１つが当たりである確率は 2/5 ずつ。
初めに選んだもの以外の4つの確率の合計は 8/5
その4つのうち１つが0であることが確定するから、残りのものが当たっている確率は　(8/5)÷3＝8/15

[解法２]
(1) 初めのものが当たっている場合(確率2/5)・・次に選ぶ３つの中に当たりが１つ
(2) 初めのものがはずれている場合(確率3/5)・・次に選ぶ３つの中に当たりが２つ

よって、求める確率＝(2/5)*(1/3)＋(3/5)*(2/3)＝8/15