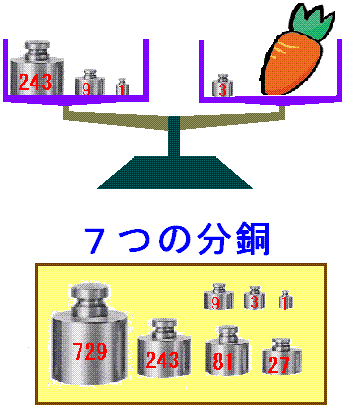
左図を見てください。1g、3g、9g、27g、81g、243g、729gの7つの分銅があります。
この、7つの分銅を用いれば、1gから1093gまで、1093種類の重さを量ることができることを知りました。
写真は、4つの分銅を用いて、人参の重さがちょうど250gであることを示したものです。
ここで、問題です。
7つの分銅のうち4つを用いて量ることの出来る重さは、1093種類のうち何種類になるでしょうか。
(※天秤の2つの皿の上には必ず4つの分銅が載っている場合で考えてください)