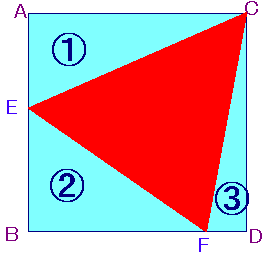
���}�̂悤�ɁA�����`�`�a�b�c������܂��B
���̒��ɐ��O�p�`�b�d�e�����܂����B
���̎��A�@�O�p�`ACE�̖ʐρF�A�O�p�`�aEF�̖ʐρF�B�O�p�`C�cF�̖ʐς�
���߂ĉ������B
�i�������A�@�ƇA�ƇB�̏��Ԃ́A�l���Ȃ����̂Ƃ���B�j

|
����聄
���}�̂悤�ɁA�����`�`�a�b�c������܂��B
�i�������A�@�ƇA�ƇB�̏��Ԃ́A�l���Ȃ����̂Ƃ���B�j |
���w�I��@
�@�����`�̂P�ӂ��P�Ƃ��āC�a�e�����Ƃ���ƁC�e�c���P�|��
�@�d�e���b�e����C�@�Q��^2���P�{�i1-���j^2�@�������āC�����|�P�{��R
�@����āC�a�e���|�P�{��R�C�e�c���Q�|��R�@����
�@�A�F�B���i�|�P�{��R�j^2�F�i�Q�|��R�j���i�S�|�Q��R�j�F�i�Q�|��R�j���Q�F�P
�Z���I��@
�@���O�p�`�̂P�ӂ��P�Ƃ���ƁC
�@�A���P�~�P���Q���Q���P�^�S
�@�@�ƇB���������āC���p�R�O���̓ӎO�p�`�b�d�e������B
�@�b�e���b�d���P�ŁC�d����b�e�ɉ��낵�������̒����͂P/�Q�E�E�E��
�@�@�@�{�B���P�~�i�P�^�Q�j���Q���P�^�S
�@����āC�A���@�{�B
���@�R�O���O�p��K�̂Q�F�P�͎Z���ł͕K�{�A�C�e���ł��B
����ƃs�^�S���X�̒藝���A
�b�d�O�Q���`�d�O�Q+�`�b�O�Q�C���Ȃ킿�A���O�Q�����O�Q+�P�A�i�P�j
�d�e�O�Q���d�a�O�Q+�a�e�O�Q�C���Ȃ킿�A���O�Q���i�P�|���j�O�Q�A
�i�Q�j�A
�����藧���܂��B
�i�P�j�i�Q�j�A�������ƁA�����Q�|��R�A�ƂȂ�܂��B
�]���āA�@�O�p�`ACE�̖ʐρF�A�O�p�`�aEF�̖ʐρF�B�O�p�`C�cF�̖ʐ�
���P�F�Q�F�P�A�ƂȂ�܂����B