「今月の問題」　第１３５　回　（平成２２年１２月）

　

＜問題＞
　
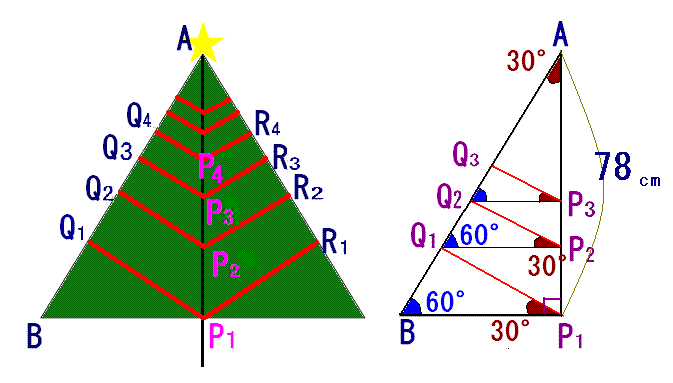
　上図のような正三角形をしたクリスマスツリーのイラストがあります。△ABP1は、∠B＝60°、
∠BAP1＝30°、ＡP1の長さが78cmです。このときの赤色をつけた枝の全ての長さを求めたいと思います。
　ただし、△ABP1、△P1BQ1、△P2Q1Q2・・・・は相似です。このようにして、木の頂点にある星まで繰り返されます。

　ここで問題です。P1Q１＋P1R１＋P2Q2＋P2R2＋P3Q3＋P3R3・・・・・は何cmになるでしょうか。
　

＜正解者一覧表＞　 　　　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１Ｍｒ.ダンディ　さん2010/12/1　0:12大阪府　
　２algebra　さん2010/12/1　0:14神奈川県　
　３マッキー２７　さん2010/12/1　0:14愛知県　
　４源内singapore　さん2010/12/1　0:16長崎　
　５kou　さん2010/12/1　0:18さいたま　
　６nak　さん2010/12/1　0:28鹿児島県　
　７男はつらいよ　さん2010/12/1　0:38神奈川県　
　８巷の夢　さん2010/12/1　7:11宮城県出身
　９信三　さん2010/12/1　7:13ゴールデンゲイトパークの隠居
１０uchinyan　さん2010/12/1　7:32東京都　
１１次郎長　さん2010/12/1　8:11兵庫県　
１２ゴンとも　さん2010/12/1　9:37豊川市　
１３AKIRA　さん2010/12/1　9:50愛知県　
１４なにわ　さん2010/12/1　9:56西宮市　
１５いちもく　さん2010/12/1　9:58立川市　
１６DAY　さん2010/12/1　10:23京都市出身　東京都在住
１７バニラ　さん2010/12/1　10:34　
１８理科ちゃんマン　さん2010/12/1　11:16理科の塾講師＠兵庫県
１９経友会の進作　さん2010/12/1　12:36京都府木津川市・72歳
２０ M'mθ　さん2010/12/1　18:21東京都　
２１川上智弘　さん2010/12/1　19:50兵庫県　
２２ ねねね　さん2010/12/1　20:22兵庫県　
２３勇水　さん2010/12/1　21:59高知県土佐山田町
２４ラスカマン　さん2010/12/1　22:03静岡県伊豆半島
２５ まいすた　さん2010/12/1　22:14　
２６ ふじも　さん2010/12/1　22:29大阪府　
２７ma-mu-ta　さん2010/12/2　0:24東京都
２８fisherman　さん2010/12/2　13:22豊岡市・塾講師
２９アゲピー　さん2010/12/2　13:25大阪
３０KAZ　さん2010/12/2　19:28熊本県
３１りーくん　さん2010/12/3　0:22埼玉県
３２oguchan1　さん2010/12/3　0:31鹿児島県
３３yossy　さん2010/12/4　9:00東京
３４AKI　さん2010/12/4　22:54山形県
３５ 鯨鯢(Keigei)　さん2010/12/5　8:11　
３６sonicASKA　さん2010/12/5　15:30神奈川県
３７ＡＢＣ４８　さん2010/12/5　20:58福島県
３８アホネン大尉　さん2010/12/8　11:21京都府
３９だだだん　さん2010/12/8　15:29東京都
４０amei　さん2010/12/8　18:30静岡県
４１やぶコウノトリ　さん2010/12/9　9:54兵庫県
４２test　さん2010/12/9　16:39　
４３まゆげにいさん　さん2010/12/9　23:16大阪府　
４４Ryosuke1998　さん2010/12/12　1:54群馬県　
４５WAKARAN　さん2010/12/12　10:16島根県　
４６阿修羅　さん2010/12/16　16:13長野県小学校教諭　
４７kasama　さん2010/12/20　10:44和歌山県プログラマ
４８みのまる　さん2010/12/21　13:40北海道　
４９すぬーぴー　さん2010/12/26　21:54横浜市　

答えは、３１２ｍでした
　
[43] 落とし穴に落ちました 投稿者：阿修羅＿２ 投稿日：2010/12/16(Thu) 16:11 [返信]

すぐに「解けた！」と思いましたが、
落とし穴に落ちました。

最後に　２倍するのを忘れていました。

　
[42] Re:[35] 無限等比級数の和の公式 投稿者：WAKARAN 投稿日：2010/12/12(Sun) 10:15 [返信]

> でできることはすぐわかりましたが最後に2倍するのを
> 忘れて正解掲示板にずっとはいれませんでした・・・

おんなじ間違いをして１週間後に......

　
[41] 今年の締め 投稿者：アゲピー 投稿日：2010/12/02(Thu) 13:33 [返信]

回答できて、上り調子

　
[40] 数列の極限？ 投稿者：fisherman 投稿日：2010/12/02(Thu) 13:32 [返信]

問題を一見たところ，数Vの「数列の極限」では？と思いましたが，難しく考えずに1:2の比を利用して(78×2）×2＝312としました。

　
[39] Re:[34] 難しく考えなくて良いんだ 投稿者：Ｍｒ.ダンディ 投稿日：2010/12/02(Thu) 10:15 [返信]

> そっか！
> p1p2はP1Q1の半分、
> するとP1Q1+P2Q2+・・・はAP1の2倍に等しい
> 右左考えて合計4倍
なるほど！
何も考えずに無限等比数列で解いてしまったのですが、・・ですね。

今年も大いに楽しませてもらい、有難うございました。

　
[38] 無題 投稿者：ひさしぶり 投稿日：2010/12/01(Wed) 22:33 [返信]

問題文が変じゃないかいな？


　
[37] 今年も感謝 Orz~来年もよろしく♪ 投稿者：スモークマン 投稿日：2010/12/01(Wed) 18:51 [返信]

あっと間に今年も最後...^^;
惜しむように遊びほうけたい〜〜〜♪

今年も楽しませていただきありがとうございました~m(_ _)m~v
来年も諸先輩方に負けじと^^;v...チャレンジ続けます!!
またよろしくで〜す Orz~~~☆☆☆

　
[36] お世話になりました・・・ 投稿者：経友会の進作 投稿日：2010/12/01(Wed) 12:41 [返信]

　72歳の歳男だやがて終わります。
今年も大変お世話になりました。
　
　来年もがんばります。

　皆様、いいお年を・・・

　
[35] 無限等比級数の和の公式 投稿者：ゴンとも 投稿日：2010/12/01(Wed) 09:34 [返信]

でできることはすぐわかりましたが最後に2倍するのを
忘れて正解掲示板にずっとはいれませんでした・・・

無限等比級数の和の公式は初項/(1-公比)だから
初項は
sqrt(3):2=x:78/sqrt(3) x=39
公比は
sqrt(3):2=z:x z=sqrt(3)*x/2
sqrt(3):2=z:sqrt(3)*x/2 z=3*x/4　より　3/4
より　公式より　39/(1-3/4)=156
この倍で156*2=312・・・・・・（答え）

　
[34] 難しく考えなくて良いんだ 投稿者：次郎長 投稿日：2010/12/01(Wed) 09:10 [返信]

何十年ぶりに等比数列とか色々考えたけど・・

そっか！
p1p2はP1Q1の半分、
するとP1Q1+P2Q2+・・・はAP1の2倍に等しい
右左考えて合計4倍
つい、難しく考えようとする。
算数で解けるからと始めたのに・・・

毎回の素晴らしい問題に感謝です