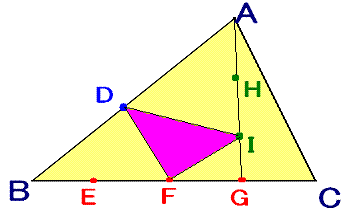
上図のような三角形ABCがあります。
点DはABの中点であり、点E、F、GはBCを4等分したものです。
また、点H、I はAGを3等分する点です。
ここで問題です。
三角形DFIの面積が4cm2のとき、元の三角形ABCの面積を求めて下さい。

「今月の問題」 (平成24年1月)

|
|
| <問題> 上図のような三角形ABCがあります。 点DはABの中点であり、点E、F、GはBCを4等分したものです。 また、点H、I はAGを3等分する点です。 ここで問題です。 三角形DFIの面積が4cm2のとき、元の三角形ABCの面積を求めて下さい。 |
 |
フォーム
を利用して、回答を下さい。
メールを利用の場合は、メールをクリックして下さい
正解者認証
※正解者掲示板に足跡を残していただけませんか。
<※1>ハンドルネームを書いて下さい!
<※2>順位表にホームページへのリンクを貼り付けていい方はURLをお書き添えください。
<※3>都道府県名や職業など知らせてもらえたら有り難いですが。
なお、締め切りは1月31 日といたします。
次回の出題予定は、平成24年2月1日 0:00を予定しています。
<正解者一覧表> 1月31日 21:00現在
| 正解者順位 | name | メール到着日時 | 備 考 |
| 1 | マッキー27 さん | 2012/1/1 0:15 | 愛知県 |
| 2 | 源内シンガポール さん | 2012/1/1 0:19 | |
| 3 | 男はつらいよ さん | 2012/1/1 0:24 | 神奈川県 |
| 4 | algebra さん | 2012/1/1 0:25 | 神奈川県 |
| 5 | まいすた さん | 2012/1/1 0:26 | |
| 6 | AKIRA さん | 2012/1/1 0:30 | 豊川市 |
| 7 | バニラ さん | 2012/1/1 0:33 | |
| 8 | kou さん | 2012/1/1 0:34 | さいたま |
| 9 | Mr.ダンディ さん | 2012/1/1 0:35 | 大阪府 |
| 10 | N.Nishi さん | 2012/1/1 0:42 | 大阪府 |
| 11 | 阿修羅 さん | 2012/1/1 0:46 | 長野県小学校教諭 |
| 12 | nak さん | 2012/1/1 0:51 | 鹿児島県 |
| 13 | 川上智弘 さん | 2012/1/1 0:56 | 兵庫県 |
| 14 | ふじも さん | 2012/1/1 1:14 | 大阪府 |
| 15 | ma-mu-ta さん | 2012/1/1 2:22 | 東京都 |
| 16 | teki さん | 2012/1/1 2:49 | 大阪府 |
| 17 | 信三 さん | 2012/1/1 3:47 | 金門公園の米寿 |
| 18 | いちもく さん | 2012/1/1 7:02 | 立川市 |
| 19 | 巷の夢 さん | 2012/1/1 7:30 | 神奈川県在住 |
| 20 | 鯨鯢(Keigei) さん | 2012/1/1 8:13 | |
| 21 | 香車 さん | 2012/1/1 8:18 | |
| 22 | 反車(Hensha) さん | 2012/1/1 8:19 | 大阪府 |
| 23 | uchinyan さん | 2012/1/1 10:19 | 東京都 |
| 24 | 次郎長 さん | 2012/1/1 10:41 | 穏やかな正月、兵庫県 |
| 25 | ラスカマン さん | 2012/1/1 11:03 | 静岡県伊豆半島 |
| 26 | cyclone さん | 2012/1/1 11:21 | 新潟 |
| 27 | wowka さん | 2012/1/1 12:43 | 静岡県 |
| 28 | 理科ちゃんマン さん | 2012/1/1 13:50 | 理科の塾講師@兵庫県 |
| 29 | ドラゴン7 さん | 2012/1/1 15:36 | 福島県郡山市 |
| 30 | のぼりん さん | 2012/1/1 15:53 | 神奈川県 |
| 31 | kanon さん | 2012/1/1 18:09 | 中学生 |
| 32 | GUTENTAG さん | 2012/1/1 22:36 | 滋賀県 |
| 33 | ISAMU さん | 2012/1/1 23:53 | 三重県 |
| 34 | ねぱ さん | 2012/1/2 0:04 | 大阪府 |
| 35 | 経友会の進作 さん | 2012/1/2 10:13 | 京都府木津川市・73歳 |
| 36 | りーくん さん | 2012/1/2 10:25 | 埼玉県 |
| 37 | 浮浪 さん | 2012/1/2 16:27 | |
| 38 | りゅう さん | 2012/1/2 19:00 | 兵庫県 |
| 39 | Liner さん | 2012/1/4 10:00 | 長野県 |
| 40 | 老人拳 さん | 2012/1/4 13:24 | 広島県 |
| 41 | KAZ さん | 2012/1/4 14:55 | 熊本県 |
| 42 | yonekiti さん | 2012/1/4 18:14 | 東京都 |
| 43 | sue さん | 2012/1/5 8:14 | 福岡県旧上津役村 |
| 44 | Michael さん | 2012/1/5 22:52 | |
| 45 | kinshicho さん | 2012/1/6 19:35 | |
| 46 | AnGeL さん | 2012/1/7 21:00 | 岡山 |
| 47 | arisu さん | 2012/1/9 17:25 | 島根県中2 |
| 48 | GBK さん | 2012/1/9 17:32 | |
| 49 | げっちゃん さん | 2012/1/9 14:31 | 北海道 |
| 50 | 浜田 明巳 さん | 2012/1/10 15:29 | |
| 51 | みなじょう さん | 2012/1/10 17:44 | 鹿児島県 |
| 52 | ゴンとも さん | 2012/1/11 22:55 | 豊川市 |
| 53 | 中学校教員 さん | 2012/1/12 12:16 | 北海道 |
| 54 | 初芝立命館高等学校 さん | 2012/1/12 16:27 | 2年4組 |
| 55 | kasama さん | 2012/1/12 13:22 | 和歌山県プログラマ |
| 56 | DAY さん | 2012/1/12 14:32 | 京都市出身東京在住 |
| 57 | tomtomtomiko さん | 2012/1/12 19:44 | 千葉県 |
| 58 | ひらたやまわき さん | 2012/1/13 0:51 | 東京 |
| 59 | 宮 さん | 2012/1/14 0:22 | 鹿児島県 |
| 60 | まんぞう さん | 2012/1/14 13:32 | おちゃ |
| 61 | ゆってぃ さん | 2012/1/20 14:21 | 埼玉 |
| 62 | ぜんざい さん | 2012/1/21 22:20 | 三重県 |
| 63 | セバス さん | 2012/1/25 13:30 | |
| 64 | ピカチュウ さん | 2012/1/26 21:30 | 兵庫県 |
| 65 | tozangezan さん | 2012/1/26 23:10 | |
| 66 | sinnta さん | 2012/1/27 16:32 | 愛知県 |
| 67 | 近藤 さん | 2012/1/27 16:39 | 神戸市長田区 |
| 68 | fどぇ さん | 2012/1/27 19:28 | |
| 69 | かず さん | 2012/1/28 4:08 | 三重県 |
| 70 | あたたた さん | 2012/1/28 9:12 | |
| 71 | やぶコウノトリ さん | 2012/1/31 9:16 | 兵庫県 |