「今月の問題」　第 １５９回　（平成２４年１２月）　　

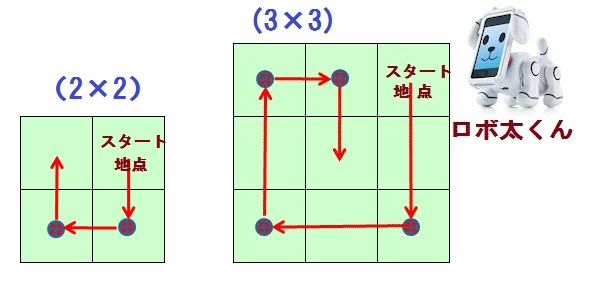
＜問題＞ 　下の図のように、ロボ太くんが正方形のかどのマス目からスタートし、正方形のマス目を時計回りに外側から内側へ１マスずつ進んでいきます。１度通ったマス目は通らないことことし、すべての、マス目を通り、最後のマス目で止まります。ロボ太くんは１マス進むのに２秒かかり、進行方向を９０°かえるのに３秒かかることが分かっています。 　例えば、（2×2）のマス目の正方形では、すべてのマス目を通るのに3マス進み、進行方向は2回変えるので、2×3＋3×2＝12秒かかります。また、（3×3）のマス目の正方形では、全てのマス目を通るのに8マス進み、進行方向を変えるのに4回変えるので、2×8＋3×4＝28秒かかります。 　ここで問題です。ロボ太君が（１０×１０）のマス目を全て通り最後のマス目にたどり着くまでに何秒かかるでしょうか。

＜正解者一覧表＞　 　

正解者順位	ｎａｍｅ	メール到着日時	備　考
１	マッキー２７　さん	2012/12/1　0:03	愛知県
２	algebra　さん	2012/12/1　0:04	神奈川県
３	二児のパパ　さん	2012/12/1　0:06	長野県
４	男はつらいよ　さん	2012/12/1　0:07	神奈川県
５	鯨鯢(Keigei)　さん	2012/12/1　0:07
６	バニラ　さん	2012/12/1　0:16	愛知県
７	源内シンガポール　さん	2012/12/1　0:18	長崎県出身
８	ラスカマン　さん	2012/12/1　0:20	静岡県伊豆半島
９	kou　さん	2012/12/1　0:21	さいたま
１０	Mr.ダンディ　さん	2012/12/1　1:32
１１	りーくん　さん	2012/12/1　2:42	埼玉県
１２	巷の夢　さん	2012/12/1　7:07	神奈川県在住
１２	香車　さん	2012/12/1　7:39
１３	次郎長　さん	2012/12/1　8:56	兵庫県
１４	uchinyan　さん	2012/12/1　15:17
１５	GUTENTAG　さん	2012/12/1　16:54	滋賀県
１６	スモークマン　さん	2012/12/1　16:55	金光＠岡山
１７	いちもく　さん	2012/12/1　17:41	立川市
１８	teki　さん	2012/12/1　20:10	大阪府
１９	のぼりん　さん	2012/12/2　0:15	東京都
２０	ゴンとも　さん	2012/12/2　1:51	豊川市
２１	中田ガウス　さん	2012/12/2　2:16
２２	塩竈人　さん	2012/12/2　4:13
２３	ma-mu-ta　さん	2012/12/2　10:44	東京都
２４	りゅう　さん	2012/12/2　12:48	兵庫県
２５	めざせ囲碁5段　さん	2012/12/2　13:13	長野県小学校教諭
２６	じゅん　さん	2012/12/2　14:37	東京
２７	たか　さん	2012/12/2　16:40	長野県
２８	まいすた　さん	2012/12/2　22:22
２９	ねぱ　さん	2012/12/3　0:09	大阪府
３０	中学校教員　さん	2012/12/3　8:10	北海道
３１	でんでん　さん	2012/12/3　9:45	千葉県
３２	まる　さん	2012/12/3　10:31	北海道
３３	Tommy　さん	2012/12/3　12:48	静岡県
３４	三貝　さん	2012/12/3　13:28	東京
３５	DAY　さん	2012/12/3　14:48	京都市在住尼崎勤務
３６	水無月　さん	2012/12/3　16:06	青森県
３７	つねまる　さん	2012/12/3　16:14	千葉県
３８	panZ　さん	2012/12/3　19:07
３９	KAZ　さん	2012/12/3　19:08	熊本県
４０	Liner　さん	2012/12/3　22:39	長野県
４１	sue　さん	2012/12/4　6:43	筑前州上津役村＠旧福岡県
４２	剛腕　さん	2012/12/4　11:18	大阪府
４３	さすらい人　さん	2012/12/4　12:36	神奈川県
４４	ao　さん	2012/12/4　14:29
４５	やぶコウノトリ　さん	2012/12/5　15：51	兵庫県
４６	南草津のトライ　さん	2012/12/5　21：56	滋賀県草津市
４７	うおっちぃ～　さん	2012/12/6　1:31	大阪府
４８	ISAMU　さん	2012/12/6　16:05	三重県
４９	ひも　さん	2012/12/7　16：41	兵庫
５０	cyclone　さん	2012/12/8　2:38	新潟県
５１	xxx　さん	2012/12/9　19:42	愛知県
５２	ふじも　さん	2012/12/9　20:13	大阪府
５２	すすきのふくろう　さん	2012/12/12　16:18	新潟県
５３	kasama　さん	2012/12/14　9:40	和歌山県プログラマ
５４	数樂　さん	2012/12/17　6:25	大阪府
５５	寒いです・１２／２１さん	2012/12/21　10:44	兵庫県
５６	oguchan1　さん	2012/12/24　17:00	鹿児島県
５７	数学者　さん	2012/12/30　10:01	東京都

答えは、２５２秒後でした。

[235] 進行方向を変える回数 投稿者：剛腕 投稿日：2012/12/04(Tue) 11:43 [返信]

この問題の核は、「進行方向を変える回数」の求め方だと思います。

nマス×nマスの正方形の場合の進行方向を変える回数をFnとすると、
F1＝0 …①
F(n＋1)＝Fn＋2 …②
となります。
(②に関しては、正方形を具体的に書いて比較してみるとわかりやすい。縦・横が１マスずつ増えると、進行方向を変える回数が２増えることがわかる。)

①②より、Fn＝F1＋2*(n－1) ←初項F1(＝0),公差2の等差数列
故に、Fn＝2*(n－1)となる。


進むマスは、n^2－1なので、
問題の一般解は、panZさんの回答の通り、2n^2＋6n－8(秒)
ちなみに、因数分解すると、2(n＋4)(n－1)

問題の答えは、これにn＝10を代入すれば求まる。

[234] panZ　さん　の回答です 投稿者：よしおか（管理人） 投稿日：2012/12/03(Mon) 19:40 [返信]

panZ　さんからメールで回答をいただきました

まず、n×nの正方形でロボタ君は、（n^2－1）マス進むことになる。ロボタ君は、1マス進むのに2秒かかるから、全てのマスを通るには、2(n^2－1)秒かかる。

また、n×nの正方形でロボタ君は、2(n－1)回方向転換しなければならない。ロボタ君は、1回方向転換するのに3秒かかるから、全ての方向転換にかかる時間は、3×2(n－1)秒、すなわち6(n－1)秒かかる。

したがって、ロボタ君の移動に必要な総時間は、
2(n^2－1)＋6(n－1)で、
2n^2＋6n－8秒。

10×10の正方形では、n=10だから、
2×10^2＋6×10－8で252秒

[232] りゅう　さん　の回答です 投稿者：よしおか（管理人） 投稿日：2012/12/02(Sun) 17:04 [返信]

（10×10）のマス目というのは、
（2×2）のマス目に、（4×4）のマス目の一番外側部分
（口の字の部分）を付け、さらに、
（6×6）のマス目の一番外側部分（口の字の部分）を付け、
（8×8）のマス目の一番外側部分（口の字の部分）を付け、
（10×10）のマス目の一番外側部分（口の字の部分）を
付けたものです。
よって、（10×10）のマス目は、4+12+20+28+36の5区画
に分割可能です。
各区画で進行方向を９０°変えるのは最後だけ２回、そ
れ以外は４回であり、マスを進む回数は（全てのマスの
数ー１）回なので、かかる時間は、
3*4*4+2*3+(100-1)*2=252(秒)

[231] 無題 投稿者：じゅん 投稿日：2012/12/02(Sun) 14:51 [返信]

５周するのに最初と最後の周は３回曲がる
途中の周回は４回曲がる
よって３×２足す４×３で１８回曲がる

通過するのは１００－１マスぶん

したがって１８×３＋９９×２＝２５２

[230] 楽しい問題グラッチェ☆ 投稿者：スモークマン 投稿日：2012/12/01(Sat) 16:52 [返信]

あっと間の１年でしたが、今年も楽しい問題のプレゼントに感謝～Orz～

今回のは角の計算がすっきりわからず...^^;
渦巻きだから...縦１０本、横９本...その角で曲がるから...
縦ー横ー縦ー横ー...-横ー縦　の間の19-1=18 なのね ^^
(100-1)*2+18*3=252
♪

[229] いつも斬新で 投稿者：次郎長 投稿日：2012/12/01(Sat) 09:02 [返信]

毎回、今回はどんな問題だろうと楽しみです。
私は9X3+8X2+7X2＋・・・で99を出してから、そうか100-1かと理解した次第で。
いつも面白い問題なので、1日の朝が楽しみです。
来年も頑張りたいものです

[228] 一年間御世話になりました 投稿者：巷の夢 投稿日：2012/12/01(Sat) 07:22 [返信]

Mr.ダンディさんと同じです。
来年も宜しくお願い申し上げます。

[227] 無題 投稿者：Mr.ダンディ 投稿日：2012/12/01(Sat) 01:44 [返信]

進む距離は　10*10ー1＝99
折れ曲がる箇所は　（１辺のマス数－１)*2＝18
よって
99＊2＋18＊3＝252 （秒）と求めました。