「今月の問題」　第１６９回　（平成２５年１０月）

　　　　　　　　　　　　　

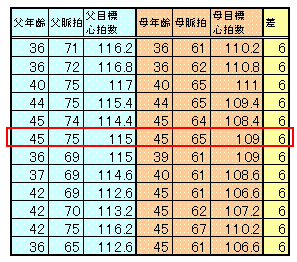
例えば、お父さんの年齢が45歳、安静時心拍数が75の時の父の目標心拍数は88-0.4×45＋0.6×75＝115
お母さんの年齢が45歳、安静時心拍数が65の時の母の目標心拍数は88-0.4×45＋0.6×65＝109
答えは115-109＝6になります。
全国の平均正答率は32.9％だったようです・
＜問題＞
左問題は、平成２５年度の全国学力学習状況調査の数学B問題です。
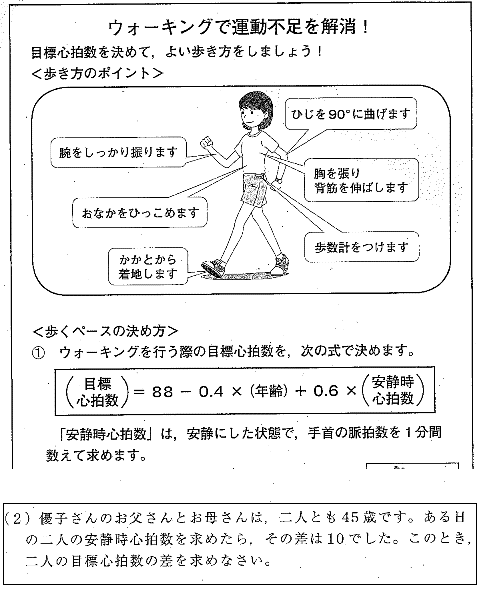
ウォーキングを行う際の目標心拍数は、
（目標心拍数）＝88-0.4×（年齢）＋0.6×（安静時心拍数）　　で表すことができるようです。


年齢と安静時心拍数には条件をつけられています。
優子さんのお父さんとお母さんの年齢は36歳以上45歳以下です。
そして、安静時心拍数は61以上75以下のどれかとします。
ここで問題です。
優子さんのお父さんお目標心拍数がお母さんの目標心拍数よりちょうど６大きくなるのは何通り考えられるでしょうか。

例えば、以下のように１２通りの場合が考えられます。

＜正解者一覧表＞　 　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１ algebra　さん 2013/10/1　1:11 神奈川県　
　２ 男はつらいよ　さん 2013/10/1　1:15 神奈川県　
　３ ＧＯＧＯＧＩＡＮＴＳさん 2013/10/1　1:19 　
　４ ゴンとも　さん 2013/10/1　4:49 豊川市　
　５ kou　さん 2013/10/1　6:09 さいたま　
　６ 巷の夢　さん 2013/10/1　8:02 神奈川県在住　
　７ バニラ　さん 2013/10/1　10:23 　
　８ 石原ゼミ　さん2013/10/1　10:41　
　９ 次郎長　さん 2013/10/1　11:42 晴天続く兵庫県　
１０ いちもく　さん 2013/10/1　17:07 立川市　
１１ 鯨鯢(Keigei)　さん2013/10/1　21:03　
１２ マッキー２７　さん 2013/10/1　21:49 愛知県　
１３ 朝霞おじさん　さん 2013/10/2　10:52 埼玉県　
１４ やぶコウノトリ　さん 2013/10/2　13:02 兵庫県　
１５ いぬたこ　さん 2013/10/3　12:58 千葉県　
１６ ねこうた　さん 2013/10/3　12:59 埼玉県　
１７ 代官山のねこ　さん 2013/10/3　13:00 東京都　
１８ 平和町の怪獣　さん 2013/10/3　13:03 愛知県　
１９ めがねおろ　さん 2013/10/3　15:21 房総　
２０ 長島しげお　さん 2013/10/3　15:31 東京都　
２１ りゅう　さん 2013/10/3　22:50 兵庫県　
２２ sue　さん 2013/10/4　6:48 筑前州上津役村＠旧福岡県
２３ cycloneの目　さん 2013/10/4　17:46 新潟県　
２４ のぼりん　さん 2013/10/4　23:24 東京都　
２５ りーくん　さん 2013/10/5　9:38 埼玉県　
２６ フォレスタのおろ　さん 2013/10/5　10:01 埼玉県　
２７ てくてくん　さん 2013/10/5　12:18 神奈川県　
２８ スモークマン　さん 2013/10/5　18:10 金光＠岡山　
２９ NNR4　さん 2013/10/6　10:21 兵庫　
３０ 蝶々婦人　さん 2013/10/7　14:08 茨城県　
３１ oguchan1　さん 2013/10/7　23:51 鹿児島県　
３２ あめい　さん 2013/10/8　16:41 静岡　
３３ Ｐｅｏｒｏ　さん 2013/10/10　15:51 千葉県　
３４ 反車(Hensha)　さん 2013/10/12　8:49 大阪府　
３５ kasama　さん 2013/10/16　15:39 和歌山県プログラマ　
３６ ISAMU　さん 2013/10/21　12:35 三重県　
３７ アール　さん 2013/10/24　8:52 　
３８ KAZ　さん 2013/10/25　16:01 熊本県　
３９ Mr.ダンディ　さん 2013/10/　 大阪府　


答えは171通りでした。

[357] 無題 投稿者：あめい 投稿日：2013/10/08(Tue) 18:39 [返信]
父－母＝０．６心拍差－０．４年齢差＝６より
（心拍差，年齢差）＝(4,-9)(6,-6)(8,-3)(10,0)(12,3)(14,6)となる組を数えました。
それぞれ
１１×１＝１１
９×　４＝３６
７×　７＝４９
５×１０＝５０
３×　７＝２１
１×　４＝　４で１７１
何度も間違えてました。

[353] 答案 投稿者：のぼりん 投稿日：2013/10/04(Fri) 23:21 [返信]
今回は、流石に算数での解決は難しそうなので、数学を使いました。

お父さんとお母さんの年齢の差を ｘ、安静時心拍数の差を ｙ とします。 題意より、
　　　－０．４ｘ＋０．６ｙ＝６
です。 両辺を五倍して移項し、
　　　３ｙ＝２（ｘ＋１５）
です。 ３ と ２ は互いに素だから、両辺は六の倍数です。 これを ６ｎ（ｎ は整数）とすれば、
　　　ｘ＝３ｎ－１５ 、　ｙ＝２ｎ
です。

年齢は ３６ 歳以上 ４５ 歳以下だから、
　　　｜ｘ｜≦１０　⇔　－１０≦３ｎ－１５≦１０　⇔　２≦ｎ≦８
です。 安静時心拍数は ６１ 以上 ７５ 以下だから、
　　　｜ｙ｜≦１５　⇔　－１５≦２ｎ≦１５　⇔　－７≦ｎ≦７
です。 双方を合わせて
　　　２≦ｎ≦７
が ｎ の範囲です。

ｎ が一つ決まったとして、お父さんとお母さんの年齢の組合せは、
　　　１０－｜ｘ｜＝１０－｜３ｎ－１５｜
　　　　＝３ｎ－５　（ｎ≦５）、　＝２５－３ｎ　（ｎ≧５）
通り、安静時心拍数の組合せは
　　　１５－｜ｙ｜＝１５－２ｎ
通りあります。

以上から、お父さんとお母さんの年齢と安静時心拍数の組合せの総数は、
　　　∑〔ｎ＝２～５〕（３ｎ－５）（１５－２ｎ）＋∑〔ｎ＝６～７〕（２５－３ｎ）（１５－２ｎ）
　　　＝１７１
通りとなりました。

[352] りゅうさん（兵庫県）の解答 投稿者：管理人 投稿日：2013/10/04(Fri) 06:32 [返信]
りゅうさん　からの解答を紹介します。

面白い問題ですが、面倒くさかった！
計算ミスをしていそうで自信がなかったのですが、一発
で掲示板に入れました。

お父さんの年齢をx1、安静時心拍数をy1、お母さんの年
齢をx2、安静時心拍数をy2とすると、
(88-0.4x1+0.6y1)-(88-0.4x2+0.6y2)
=-0.4(x1-x2)+0.6(y1-y2)=6
お父さんとお母さんの年齢差をa、お父さんとお母さん
の安静時心拍数の差をbとすると、
-0.4a+0.6b=6
-9≦a≦9
-14≦b≦14
これに当てはまるa,bの組み合わせは、
①a=-6,b=14
これに該当する(x1,x2,y1,y2)は、
(36,42,75,61),(37,43,75,61),(38,44,75,61),(39,45,75,61)
全部で4通り
②a=-3,b=12
これに該当する(x1,x2,y1,y2)は、
(36,39,75,63),(37,40,75,63),(38,41,75,63),...,(42,45,75,63),
(36,39,74,62),(37,40,74,62),(38,41,74,62),...,(42,45,74,62),
(36,39,73,61),(37,40,73,61),(38,41,73,61),...,(42,45,73,61)
全部で7*3=21通り
③a=0,b=b=10
これに該当する(x1,x2,y1,y2)は、
(36,36,75,65),(37,37,75,65),(38,38,75,65),....,(45,45,75,65),
(36,36,74,64),(37,37,74,64),(38,38,74,64),....,(45,45,74,64),
.....
(36,36,71,61),(37,37,71,61),(38,38,71,61),....,(45,45,71,61)
全部で10*5=50通り
④a=3,b=8
これに該当する(x1,x2,y1,y2)は、
(39,36,75,67),(40,37,75,67),(41,38,75,67),....,(45,42,75,67),
(39,36,74,66),(40,37,74,66),(41,38,74,66),....,(45,42,74,66),
.....
(39,36,69,61),(40,37,69,61),(41,38,69,61),....,(45,42,69,61)
全部で7*7=49通り
⑤a=6,b=6
これに該当する(x1,x2,y1,y2)は、
(42,36,75,69),(43,37,75,69),(44,38,75,69),(45,39,75,69),
(42,36,74,68),(43,37,74,68),(44,38,74,68),(45,39,74,68),
.....
(42,36,67,61),(43,37,67,61),(44,38,67,61),(45,39,67,61)
全部で4*9=36通り
⑥a=9,b=4
これに該当する(x1,x2,y1,y2)は、
(45,36,75,71),(45,36,74,70),(45,36,73,69),...,(45,36,65,61),
全部で11通り

合計では、
4+21+50+49+36+11=171（通り）


[351] 数学的でないですが 投稿者：いぬたこ 投稿日：2013/10/03(Thu) 12:57 [返信]
整数になる組み合わせを地道に解きました。
[350] Re:[348] 問題文について 投稿者：管理人 投稿日：2013/10/02(Wed) 07:58 [返信]
> 問題文の「年齢は36歳から45歳の間」「安静時心拍数は61から75の間」が気になります。
> 「間」というのは、普通、両端を含みません。

国語力がなくて恥ずかしい限りです。訂正させていただきました。

今回の全国学力調査の問題は、変数を固定することで中学校２年生で学習する１次関数の式になることを意図されたものだと思います。

変数を２つにすると、如何に大変になるかということを改めて感じさせられました。
解答を送っていただけた皆様本当にありがとうございます。

[347] 確かに、いつもと違う・・ 投稿者：次郎長 投稿日：2013/10/01(Tue) 11:46 [返信]

巷の夢さん同様、私もいつもと違うなと感じながら取り組みました。落ち着いてやれば難しい訳ではないですが、いつも書き散らす私には少々面倒でした。
でもこういう問題は私は好きです。

いつも面白い問題に感謝しています

[346] 十進basic で 投稿者：ゴンとも 投稿日：2013/10/01(Tue) 08:36 [返信]
優子さんのお父さんの年齢,安静時心拍数をそれぞれa,b
お母さんの年齢,安静時心拍数をそれぞれa1,b1として

let s=0
FOR a=36 TO 45
FOR b=61 TO 75
FOR a1=36 TO 45
FOR b1=61 TO 75
if 88-0.4*a+0.6*b=88-0.4*a1+0.6*b1+6 then let s=s+1
next b1
next a1
next b
next a
print s
END

f9押して　171通り・・・・・・(答え)

[345] いつもと違う・・・・？ 投稿者：巷の夢 投稿日：2013/10/01(Tue) 08:08 [返信]
いつもと違い結構面倒でした。最初、頭の中で計算しておりましたが、こんがらがってしまい、きちんと方程式をたて、場合わけして解きました。この場合訳が６種類もあり、結構疲れましたが、正解に至り、満足々・・・・。