「今月の問題」　第１７１回　（平成２５年１２月）

＜問題＞
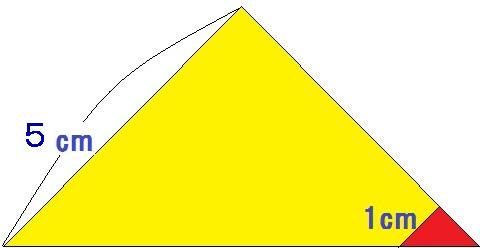
　右図を見てください。
　直角をはさむ辺の長さが５cmの直角二等辺三角形です。
　　この直角二等辺三角形を、直角をはさむ辺の長さが1cmの直角二等辺三角形で並べ替えて埋め込むことを考えています。

　ここで問題です。並べ方については、何通りあるでしょうか。


　小学校１年生の算数の教科書の問題から出題しました。
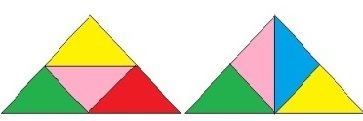
　直角二等辺三角形を並べ替えていろいろな形作りをする問題が出題されていました。
　下図は、直角をはさむ辺の長さが２cmの直角二等辺三角形を1辺１cmの直角三角形で並べかえて作るには２つの方法があることを子どもは直ぐに見つけたのには驚きでした。
　（簡単すぎるぞーと聞こえて来るようですが・・・）

＜正解者一覧表＞　 　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１ kou　さん 2013/12/1　0:02 さいたま　
　２ 源内シンガポール　さん2013/12/1　0:03長崎県　
　３ マッキー２７　さん 2013/12/1　0:09 愛知県　
　４ kuro　さん 2013/12/1　0:10 北海道　
　５ cycloneの目　さん 2013/12/1　0:22 新潟　
　６ バニラ　さん 2013/12/1　0:31 　
　７ いちもく　さん 2013/12/1　6:37 立川市　
　８ 鯨鯢(Keigei)　さん2013/12/1　7:01　
　９ 巷の夢　さん 2013/12/1　7:27 神奈川県在住　
１０ 次郎長　さん 2013/12/1　8:32 冷える兵庫県　
１１ algebra　さん 2013/12/1　9:39 神奈川県　
１２ 香車　さん 2013/12/1　18:59 　
１３ AKIRA　さん 2013/12/1　19:07 愛知県　
１４ まいすた　さん2013/12/1　19:14　
１５ Mr.ダンディ　さん 2013/12/1　20:27 愛知県　
１６ 男はつらいよ　さん 2013/12/1　21:16 神奈川県　
１７ まいすた石原ゼミ　さん2013/12/1　22:52　
１８ いぬたこ　さん 2013/12/2　9:56 千葉県　
１９ ねこ　さん 2013/12/2　9:58 埼玉県　
２０ うた　さん 2013/12/2　9:59 東京渋谷　
２１ 平和町の怪獣　さん 2013/12/2　9:59 愛知県　
２２ 代官山のアジアンカフェ　さん 2013/12/2　10:24 千葉県茂原市　
２３ きむちん　さん 2013/12/2　11:44 あきた　
２４ たこさんぐん　さん 2013/12/2　11:47 広島県　
２５ やぶコウノトリ　さん 2013/12/2　13:56 兵庫県　
２６ KAZ　さん 2013/12/2　14:57 熊本県　
２７ 車輪剣！　さん 2013/12/2　15:38 千葉県　
２９ uchinyan　さん 2013/12/2　16:00 　
３０ 織田信長の子孫　さん 2013/12/2　16:27 神奈川県　
３１ ゆずぽん　さん 2013/12/2　22:02 　
３２ NNR4　さん 2013/12/2　23:09 兵庫県　
３３ めざせ囲碁５段　さん 2013/12/3　10:07 長野県小学校教諭　
３４ ２＋２＝５　さん 2013/12/3　10:18 大阪府　
３５ 猫魂　さん 2013/12/3　19:14 宮崎　
３６ 朝霞おじさん　さん 2013/12/4　14:07 埼玉県　
３７ 理科ちゃんマン　さん 2013/12/4　18:55 理科の塾講師＠兵庫県　
３８ 小学生　さん 2013/12/4　22:13 　
３９ Jママ　さん 2013/12/5　6:09 　
４０ いぬい　さん 2013/12/5　12:15 滋賀県　
４１ アール　さん 2013/12/5　17:09 　
４２ 中田ガウス　さん 2013/12/6　12:59 　
４３ 反車(Hensha)　さん 2013/12/6　16:52 大阪府　
４４ りゅう　さん 2013/12/6　21:47 兵庫県　
４５ てくてくん　さん 2013/12/7　12:35 　
４６ あ　さん 2013/12/7　23:12 　
４７ pao　さん 2013/12/8　22:59 　
４８ まる　さん 2013/12/17　12:27 北海道　
４９ GUTENTAG　さん 2013/12/17　13:25 滋賀県
５０ うおっちぃ～　さん 2013/12/19　12:16 大阪府　
５１ つねまる　さん 2013/12/19　17:36 千葉県　
５２ スモークマン　さん 2013/12/27　13:59 金光＠岡山　
５３ りーくん　さん 2013/12/28　16:09 埼玉県　
５４ SAMU　さん 2013/12/29　9:58 三重県　
５４ SAMU　さん 2013/12/29　9:58 三重県　
５５ ゴンとも　さん 2013/12/29　19:53 豊川市　

答えは　1024個です。

[381] 無題 投稿者：ゆづぽん 投稿日：2013/12/02(Mon) 22:02 [返信]
先月から参加させて頂いております。
三角形の辺の長さを2,3,4,5と伸ばしていくことで規則性を見つけました。それぞれ1,3,6,10と数列のように正方形が出てくるのですね。面白い問題をありがとうございます。
[380] できた！ 投稿者：いぬたこ 投稿日：2013/12/02(Mon) 09:56 [返信]
数列、帰納法的ですね。
[379] 一般化すると 投稿者：Mr.ダンディ 投稿日：2013/12/01(Sun) 20:44 [返信]
今月の問題は
直角三角形の1辺が　ｎ（ｃｍ）（ｎ≧2）のときは
2＾{n(n-1)/2} 通り
と一般化できますね。
《本年度も楽しい問題を有り難うございました》
[378] 引っ掛けは無いらしい 投稿者：まいすた 投稿日：2013/12/01(Sun) 19:14 [返信]
大三角の５ｃｍの辺に接する小三角の辺は、１ｃｍの場合と√２ｃｍの場合が考えられます。
ただし、１つ以上の√２ｃｍの辺といくつかの１ｃｍの辺を組み合わせてちょうど５ｃｍにすることは出来ません。
よって、大三角の５ｃｍの辺に接する小三角の辺は１ｃｍのみと分かります。同様に考えると、１ｃｍの辺は必ず斜めになっていなければいけないと分かります。
すると、小三角２つでできる正方形は１０個なので、２＾１０となります。
[377] 面白かったです 投稿者：次郎長 投稿日：2013/12/01(Sun) 08:38 [返信]
おはようございます。
私も単純に2^10としましたが、こういう問題は、いや、それでもこんな場合があるよというのが出てこないかと．．．そんな気持ちが捨てきれません
来年もまだがんばれそうです。
[376] 2㎝の場合がヒントですね・・・・ 投稿者：巷の夢 投稿日：2013/12/01(Sun) 07:36 [返信]
例題のように三角形の長さを１cmずつ増やしていくと・・・、
規則性が現れて・・・・。
本年も色々とお世話になりました。来年も宜しくご指導のほど
お願い申し上げます。
[375] 四角形が10個で 投稿者：cycloneの目 投稿日：2013/12/01(Sun) 00:24 [返信]
同じく2^10です
[374] 無題 投稿者：kuro 投稿日：2013/12/01(Sun) 00:09 [返信]
縦並びか横並びかがどちらでもよい場所が１０カ所
ということで
２の１０乗ですね