「今月の問題」　第１１回　（平成１２年８月）

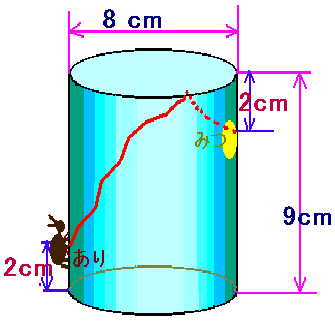
右図のような、底面の直径が８ｃｍ、高さが９ｃｍの円柱形のコップがある。
このコップの外側の下から２ｃｍの所に「あり」がいます。
また、「あり」の真反対のコップの内側に「ハチミツ」がついています。
「ハチミツ」の位置は、コップの上から２ｃｍの所です。
「あり」が「ハチミツ」の位置まで最短距離で歩いて行くとき、その道のりは何ｃｍになるでしょうか。

ただし、円周率は３として計算して下さい。

答は１５ｃｍです。
「畠山」さんの解答です
ありの位置を点P,みつの位置を点Qとする。
点Pを通り、底面に垂直な直線に沿った直線を考え、この直線と上面との 交点を点A,下面との交点を点Bとする。
同様に点Qを通り底面に垂直な直線と上面、下面との交点をそれぞれ 点D,Cとする。
問題は四角形ABCDにおいて辺AB上にある点Pを出発して辺ADと交差し、 辺CD上にある点Qに至るまでの最短距離を求める問題として扱うことと 同義である。

求める距離をlとする。
点Pは四角形ABCDの辺AB上にあり、BP=2cm
点Qは辺CD上にあり
QD=2cm
また辺AD,BCは底面の円周の1/2であるから
AD=BC=4πcm、
また
AB=CD=9cm
である。

辺ADを対称軸として、四角形ABCDを折り返す。点B,C,Qに対応する
点をそれぞれB',C',Q'とする(四角形ABCDがコップの外側の面、
四角形AB'C'Dがコップの内側の面に対応する)と、
l=PQ'
であり、また
QD=Q'D=2cm
であるから、

l^2=AD^2+(AP+Q'D)^2
=(4π)^2+(9-2+2)^2
=16π^2+81
πを3として計算するから、
l^2=16*9+81
=225
したがってl=15cmである。

「かつひこ」さん「BossF」さん他
最短距離は直線に進むことなので、「裏面の上から２ｃｍのところ＝円柱の２ｃｍ上 のところ」と考えて、円柱の展開図を書きました。
すると求めたい距離は２辺が１２ｃｍ、９ｃｍの直角三角形の斜辺になります。

その他「ごま姫」さんからは、GIFファイルで分かりやすい説明図を頂きましたので、希望があればメールでお知らせします。