�@�u�����̖��v�@��P�Q��@�i�����P�Q�N�X���j
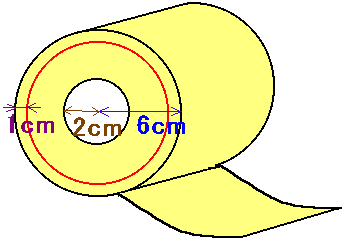
�E�}�̂悤�ȁA�O���̔��a���U�����A�����̔��a���Q�����̃g�C���b�g�y�[�p�[������B
���̃g�C���b�g�y�[�p�[���X���P���Ɏg���n�߂��Ƃ���A���傤�ǂP�O���ԂŊO������P�����̏��܂��g�����Ƃ����B
���̉Ƒ��́A����ɂU�U�O�����g�����Ƃ��������Ă���B
����g�C���b�g�y�[�p�[�����ւ�����́A���������ł��傤���B
�i�����܂���聄�g�C���b�g�y�[�p�[�̌��������߂ĉ�����Ί������ł��B�j
�������A�~�����͂R�Ƃ��Čv�Z���ĉ������B
|
 |
�����́A�X���R�O���ł��B
�I�}�P���̓����͂O�D�O�T�����ł����B
<tomo����̉�
�ł���
36��-25��=11��
25��-4��=21��
21��/1.1��=19.0909....
���ƂP�X���ԂԂ�Ə����c��܂��B
10+19=29
������@�X���R�O���ł��B
������a n�����Ƃ����
��������
�P���ځE�E�E2(2+a)��=6(2+a)=12+6a
�Q���ځE�E�E2(2+2a)��=6(2+2a)=12+6a*2
�R���ځE�E�E2(2+3a)��=6(2+3a)=12+6a*3
�E
�E
�����ځE�E�E2(2+na)��=6(2+na)=12+6a*n
�ȏ�̑��a��19200cm�E�E�E�Email�ʼnς�
12n+6a(1+2+3+.........+n)=19200...........�@
na=4...........�A
�@���@�@�@12n+6a*n(n+1)/2=19200.......�B
�B�ɇA�������� 12n+12(n+1)=19200.....�C
�A�C���@�@a=0.005003126.......
�]���Ď��̌����͖�@�@0.005cm
���[���͖�@�@�@800��
���l�c���܁A���������ABossF���܂̉ł���
�P�O���ԂŎg�����g�C���b�g�y�[�p�[�̑��ʐς́C
�@�@�U^2�|(�U�|�P)^2���P�P�icm2�j
�@�̂ɂP���ԂŎg�����g�C���b�g�y�[�p�[�̑��ʐς́C
�@�@�P�P���P�O���P.�P�icm2�j
�@�g�C���b�g�y�[�p�[�S�̂̑��ʐς́C
�@�@�U^2�|�Q^2���R�Q�icm2�j
�@�̂Ɏg��������́C
�@�@�R�Q���P.�P���R�Q�O�^�P�P���Q�X.�O�X�c�c
�@�̂ɂR�O���ځC���Ȃ킿�X���R�O���ɓ���ւ��邱�ƂɂȂ�D
�@�܂��C�g�C���b�g�y�[�p�[�̌��������p�Ƃ���ƁC�P���Ɏg���g�C��
�b�g�y�[�p�[�̑��ʐς́C
�@�@�U�U�O�~�����P.�P���P.�P�~�R
�@�@�������O.�O�O�T
�@�̂Ƀg�C���b�g�y�[�p�[�̌��݂͂O.�O�O�Tcm�ł���
���j�d�m���܂̉�
���̕���l[cm],������d[cm]�Ƃ���B
10���ԂŎg�p�������̑̐ς�
(6^2-5^2)��l[cm^3] (1) (���[������̌v�Z)
660dl*10[cm^3] (2) (1���̎g�p�ʂ���v�Z)
(1),(2)���
11��l=6600dl
�ƂȂ�A��=3�Ƃ��Čv�Z�����
d=0.005 [cm] (3)
�ŏ��ɂ��������̑̐ς�(6^2-2^2)��l[cm^3]�ł��邩��
���[�����g������̂ɕK�v�ȓ�����t�Ƃ����
(6^2-2^2)��l=660dlt
�ƂȂ�B(3)��p�����
32��=3.3t
�ł���A��=3�Ƃ��Čv�Z�����
t=320/11�`29.1 [��]
�ƂȂ�B���������āA���Ɍ�������̂�9��30���ł���B
���̑��A�������u���ܕP�v����́A������₷���摜�Ő������Ă��������܂����B
��]���Ă��������܂��Ƒ��点�Ē����܂��B
�@
