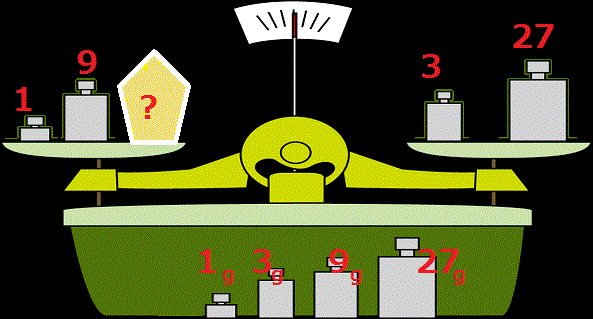
下図を見て下さい。上皿天秤と1g、3g、9g、27gの4つの分銅があります。
これらの4つの分銅のいくつかを利用すれば、1gから40gの全てを量るとができることが分かりました。
下図のように置けば、20gを量ることができます。
ここで問題です。
4つの分銅全てを、左右のどちらかの上皿にのせて量る重さは、1から40gのうち何通りになるでしょうか。
※40g(40通り)のうち4個の分銅を使わなければ、量ることのできない重さを数え上げて下さい。いつもながら題意が不明瞭で申し訳ありません。
|
<問題> 下図を見て下さい。上皿天秤と1g、3g、9g、27gの4つの分銅があります。 これらの4つの分銅のいくつかを利用すれば、1gから40gの全てを量るとができることが分かりました。 下図のように置けば、20gを量ることができます。 ここで問題です。 4つの分銅全てを、左右のどちらかの上皿にのせて量る重さは、1から40gのうち何通りになるでしょうか。 ※40g(40通り)のうち4個の分銅を使わなければ、量ることのできない重さを数え上げて下さい。いつもながら題意が不明瞭で申し訳ありません。 |
|
 |
|
<正解者一覧表>
| 順 位 |
name | メール到着日時 | 備 考 |
| 1 | 鯨鯢(Keigei) さん | 2015/1/1 0:03 | |
| 2 | 物理好き さん | 2015/1/1 0:05 | |
| 3 | kou さん | 2015/1/1 0:06 | さいたま |
| 4 | AKIRA さん | 2015/1/1 0:08 | 愛知県 |
| 5 | マッキー27 さん | 2015/1/1 0:09 | 愛知県 |
| 6 | Mr.ダンディ さん | 2015/1/1 0:17 | 大阪府 |
| 7 | algebra さん | 2015/1/1 0:32 | 神奈川県 |
| 8 | 男はつらいよ さん | 2015/1/1 0:33 | 神奈川県 |
| 9 | 次郎長 さん | 2015/1/1 0:56 | 次郎長 |
| 10 | tt さん | 2015/1/1 0:57 | |
| 11 | ゴンとも さん | 2015/1/1 1:45 | 豊川市 |
| 12 | 朝霞おじ さん | 2015/1/1 4:34 | 埼玉県 |
| 13 | ユートニウム さん | 2015/1/1 6:57 | |
| 14 | 猫魂 さん | 2015/1/1 9:20 | 宮崎県 |
| 15 | スモークマン さん | 2015/1/1 12:58 | 岡山 |
| 16 | バニラ さん | 2015/1/1 13:00 | |
| 17 | りーくん さん | 2015/1/1 13:24 | 埼玉県 |
| 18 | GUTENTAG さん | 2015/1/1 13:57 | 滋賀県 |
| 19 | sue さん | 2015/1/1 15:40 | 筑前州上津役村@旧福岡県 |
| 20 | ltsu さん | 2015/1/1 16:30 | 大阪府小5 |
| 21 | uchinyan さん | 2015/1/1 22:03 | |
| 22 | teki さん | 2015/1/1 22:18 | 大阪府 |
| 23 | ペンギン さん | 2015/1/2 2:58 | 東京都 大学生 |
| 24 | いちもく さん | 2015/1/2 5:08 | 立川市 |
| 25 | 石原ゼミさん | 2015/1/2 16:48 | 兵庫県 |
| 26 | たかひろ さん | 2015/1/3 9:58 | 埼玉県 |
| 27 | カルダノ さん | 2015/1/3 16:16 | 群馬県 |
| 28 | アール さん | 2015/1/4 20:14 | |
| 29 | ??? さん | 2015/1/5 9:00 | |
| 30 | 虹パパ さん | 2015/1/5 15:13 | 東京都 |
| 31 | 巷の夢 さん | 2015/1/6 9:12 | 神奈川県在住 |
| 32 | つねまる さん | 2015/1/6 13:12 | 千葉県 |
| 33 | あめい さん | 2015/1/6 17:01 | |
| 34 | 元気モリモリ さん | 2015/1/6 17:23 | 宮崎県 |
| 35 | KAZ さん | 2015/1/6 19:16 | 熊本県 |
| 36 | 剛腕 さん | 2015/1/6 20:58 | 大阪府 会社員 |
| 37 | やぶコウノトリ さん | 2015/1/7 11:46 | 兵庫県 |
| 38 | NNR4 さん | 2015/1/8 20:57 | 兵庫県 |
| 39 | 士郎・p・部分群 さん | 2015/1/10 2:17 | 美食倶楽部 |
| 40 | ラスカマン さん | 2015/1/10 20:01 | 静岡県伊豆半島 |
| 41 | 南草津のトライ さん | 2015/1/15 15:36 | 滋賀 |
| 42 | 岡本ボンバーズ さん | 2015/1/19 10:15 | 秋田県 |
| 43 | なにわともあれ さん | 2015/1/29 11:42 | 岩手県 |
| 44 | TK さん | 2015/1/31 19:01 | 埼玉県 |
答えは 8通りでした。