「今月の問題」 第185回 (平成27年2月)
<問題>
リアクション芸人の出川哲朗さんの生年月日は、1964年2月13日です。自ら 「汚れ役」に挑戦し人気を持続しています。
13日の金曜日は、不吉な日として忌み嫌われていますが、出川さんにとっては、幸運をもたらすと考えておられるかもしれません。今月13日は金曜日になります。
ここで問題です。
出川さんが出生された1964年2月13日から数えて、平成27年2月13日は、何回目の13日の金曜日になるでしょうか。
※「13日の金曜日」は2月とは限っていません。今月も読み取りにくい問題文でごめんなさい。 |
 |
 |
<正解者一覧表>
| 順位 |
name |
メール到着日時 |
備 考 |
| 1 |
男はつらいよ さん |
2015/2/1 0:08 |
神奈川県 |
| 2 |
ゴンとも さん |
2015/2/1 0:16 |
豊川市 |
| 3 |
kou さん |
2015/2/1 0:17 |
さいたま |
| 4 |
川上智弘 さん |
2015/2/1 0:35 |
兵庫県 |
| 5 |
葉月エミリー さん |
2015/2/1 0:41 |
東京 |
| 6 |
バニラ さん |
2015/2/1 1:29 |
|
| 7 |
鯨鯢(Keigei) さん |
2015/2/1 7:37 |
http://blogs.yahoo.co.jp/oka_yadokary |
| 8 |
TK さん |
2015/2/1 8:30 |
埼玉県 |
| 9 |
いちもく さん |
2015/2/1 8:38 |
立川市 |
| 10 |
次郎長 さん |
2015/2/1 8:39 |
寒い中、墓参り、兵庫県 |
| 11 |
ユートニウム さん |
2015/2/1 9:25 |
|
| 12 |
りーくん さん |
2015/2/1 10:24 |
埼玉県 |
| 13 |
物理好き さん |
2015/2/1 10:26 |
|
| 14 |
uchinyan さん |
2015/2/1 12:13 |
東京都 |
| 15 |
algebra さん |
2015/2/1 17:04 |
神奈川県 |
| 16 |
OGOGIANTS さん |
2015/2/1 18:04 |
|
| 17 |
石原ゼミ さん |
2015/2/1 19:21 |
http://i-semi.jp/ |
| 18 |
朝霞おじさん さん |
2015/2/1 20:19 |
埼玉県 |
| 19 |
NNR4 さん |
2015/2/1 20:55 |
兵庫県 |
| 20 |
マッキー27 さん |
2015/2/1 21:00 |
愛知県 |
| 21 |
teki さん |
2015/2/1 22:16 |
大阪府 |
| 22 |
アール さん |
2015/2/2 9:41 |
|
| 23 |
あめい さん |
2015/2/2 13:42 |
|
| 24 |
スモークマン さん |
2015/2/2 19:07 |
|
| 25 |
??? さん |
2015/2/4 9:21 |
滋賀県 |
| 26 |
GUTENTAG さん |
2015/2/4 14:36 |
滋賀県 |
| 27 |
やぶコウノトリ さん |
2015/2/4 15:30 |
兵庫県 |
| 28 |
のぼりん さん |
2015/2/4 21:39 |
|
| 29 |
巷の夢 さん |
2015/2/4 22:14 |
|
| 30 |
理科ちゃんマン さん |
2015/2/9 17:21 |
理科の塾講師@兵庫県 |
| 31 |
老人拳 さん |
2015/2/23 13:49 |
広島 |
| 32 |
Mr.ダンディ さん |
2015/2/26 12:27 |
大阪府 |
答えは 87でした
[
16]
んんん・・・ 投稿者:
Mr.ダンディ <3gatu>
投稿日: 2015/02/26(Thu) 12:25
今回の問題の限り 食指が動かず、締め切り近くまで放置していました。
結局
鯨鯢(Keigei)さんと同じような表をつくって数えることになりました。
[
14]
上手い解法は? 投稿者:
のぼりん <3gatu> 投稿日:
2015/02/04(Wed) 21:39
上手い解法はないものでしょうか?
曜日問題となると、Zeller の公式程度しか思い付く道具がないですが、
Gauß
記号満載なので、代数方程式の様に解くことができません。
結局、虱潰しになってしまいました。
[
13]
Re:[12] 適当です。確かに 投稿者:
次郎長
<3gatu> 投稿日: 2015/02/03(Tue) 21:13
とんでもないです
私はいつもベラメェ推定で^^;;
> なるほど^^☆
> プチフェルミ推定ですね♪
> わたし?…黙秘…^^;;
[
12]
Re:[9] 適当ですが 投稿者:
スモークマン <3gatu> 投稿日:
2015/02/02(Mon) 19:07
> 13日は1年に12回、金曜日は7日に1回
> なら、1年に13日の金曜日は12/7回
> 52年×12/7==約89回
> さぁ、認証だ、89ダメ、。88ダメ、87おっ開いた。
なるほど^^☆
プチフェルミ推定ですね♪
わたし?…黙秘…^^;;
[
11]
無題 投稿者:
あめい <3gatu> 投稿日:
2015/02/02(Mon) 13:40
平年の正月が月~日の13日の金曜日は2,2,1,3,1,1,2回。閏年は2,1,2,2,1,1,3回。これと出して下さった表で。
[
10]
無題 投稿者:
物理好き <3gatu> 投稿日:
2015/02/01(Sun) 11:00
<平年>
1/1をg曜日(月~日をa~gに置き換えてどれでも入るようにする)
とすると、
abcdefg
2694158
3ー12710ーー
11ーーーーーー
↑これはn月13日が何曜日にあたるかを示したカレンダーです。
金曜||↓年(西暦下2桁)
g=日e6778899506--・・・2×5
g=月d7379900107--・・・2×5
g=火c7485910213--・・・2×5
g=水b697586970314・・・1×6
g=木a7081879809--・・・3×5
g=金g657182939910・・・1×6
g=土f667783940511・・・1×6
計63回
<閏年>
平年と同様に
abcdefg
23691105
811-124-----
--------7-----
金曜||年(西暦下2桁)
g=日e8412・・・3×2
g=月d6896・・・2×2
g=火c8008・・・1×2
g=水b92--・・・2×1
g=木a7604・・・2×2
g=金g88--・・・1×1
g=土f7200・・・1×2
計21回
<1964>
2月からなので2回。
<2015>
2月までなので1回。
63+21+2+1=87
2015/2/13は1964/2/13から数えて87回目の「13日の金曜日」。
[
9]
適当ですが 投稿者:
次郎長 <3gatu> 投稿日:
2015/02/01(Sun) 08:44
13日は1年に12回、金曜日は7日に1回
なら、1年に13日の金曜日は12/7回
52年×12/7==約89回
さぁ、認証だ、89ダメ、。88ダメ、87おっ開いた。
[
8]
13日の金曜日 投稿者:
鯨鯢(Keigei) <3gatu>
投稿日: 2015/02/01(Sun) 08:07
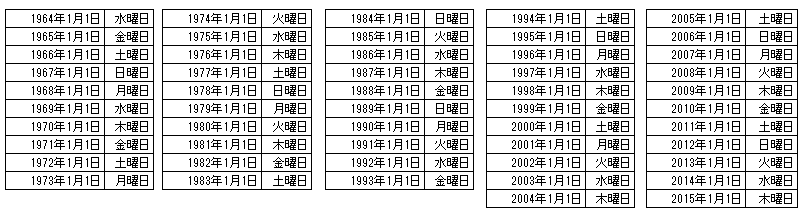
1月1日の曜日と 13日が金曜日になる月の関係は、次のようになります。
平年は、日⇒ 1,10,月⇒ 4,7,火⇒ 9,12,水⇒
6,木⇒ 2,3,11,金⇒ 8,土⇒ 5
閏年は、日⇒ 1,4,7,月⇒ 9,12,火⇒ 6,水⇒ 3,11,木⇒ 2,8,金⇒
5,土⇒ 10
また、28年毎に、1月1日の曜日は何れも 平年が3回ずつ,閏年が1回ずつで、
13日の金曜日は全体の 1/7
で、28×12÷7=48 回ですので、
1964年~2019年の56年間に 96回、このうち、2015年3月~2019年を除けば良い。
1月1日の曜日は 2015年(木),2016年(金),2017年(日),2018年(月),2019年(火) で、
2016年が閏年であることに注意し、13日の金曜日は、3回,1回,2回,2回,2回の 10回、
2015年の2月を含めるから、96-10+1=87回です。



