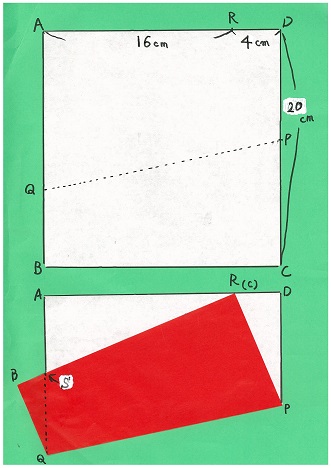
右図のような1辺が20cmの正方形ABCDの折り紙があります。
今、辺AB上に点Q,CD上に点Pをとり,直線PQを折り目として正方形を折ったところ点CがAD上の点Rに重なりました。
AR:RD=4:1になり、つまり、AR=16cm、RD=4cmになります。
ここで問題です。
赤色の四角形CBQPの面積は何cm2になるでしょうか。
|
<問題> 右図のような1辺が20cmの正方形ABCDの折り紙があります。 今、辺AB上に点Q,CD上に点Pをとり,直線PQを折り目として正方形を折ったところ点CがAD上の点Rに重なりました。 AR:RD=4:1になり、つまり、AR=16cm、RD=4cmになります。 ここで問題です。 赤色の四角形CBQPの面積は何cm2になるでしょうか。 |
 |
<正解者一覧表>
| 順位 | name | メール到着日時 | 備 考 |
| 1 | algebra さん | 2015/6/1 0:05 | 神奈川県 |
| 2 | Mr.ダンディ さん | 2015/6/1 0:10 | 大阪府 |
| 3 | 男はつらいよ さん | 2015/6/1 0:13 | 神奈川県 |
| 4 | kou さん | 2015/6/1 0:18 | さいたま |
| 5 | ゴンとも さん | 2015/6/1 0:19 | 豊川市 |
| 6 | 朝霞おじさん さん | 2015/6/1 0:25 | 埼玉県 |
| 7 | AKIRA さん | 2015/6/1 0:37 | |
| 8 | バニラ さん | 2015/6/1 1:07 | |
| 9 | いちもく さん | 2015/6/1 5:21 | 立川市 |
| 10 | 鯨鯢(Keigei) さん | 2015/6/1 5:28 | 埼玉県 |
| 11 | 巷の夢 さん | 2015/6/1 5:47 | 神奈川県在住 |
| 12 | 次郎長 さん | 2015/6/1 7:41 | 夜寒く昼は暑い兵庫県 |
| 13 | いぬたこ さん | 2015/6/1 10:05 | 千葉県 |
| 14 | うたねこ さん | 2015/6/1 10:06 | 栃木 |
| 15 | uchinyan さん | 2015/6/1 11:33 | 東京都 |
| 17 | GUTENTAG さん | 2015/6/1 15:08 | 滋賀県 |
| 18 | やぶコウノトリ さん | 2015/6/1 15:22 | 兵庫県 |
| 19 | hiroki さん | 2015/6/1 16:40 | 東京都 |
| 20 | マッキー27 さん | 2015/6/1 20:51 | 愛知県 |
| 21 | ユートニウム さん | 2015/6/1 20:56 | |
| 22 | NNR4 さん | 2015/6/1 21:07 | 兵庫 |
| 23 | まいすた さん | 2015/6/1 23:36 | |
| 24 | sue さん | 2015/6/2 6:48 | 筑前州上津役村@旧福岡県 |
| 25 | 南草津のトライプラス さん | 2015/6/2 15:37 | 滋賀 |
| 26 | ??? さん | 2015/6/2 17:27 | |
| 27 | つねまる さん | 2015/6/2 18:40 | 千葉県 |
| 28 | スモークマン さん | 2015/6/2 21:10 | @新倉敷 |
| 29 | たかひろ さん | 2015/6/2 22:10 | 埼玉県 |
| 30 | perry さん | 2015/6/3 22:46 | |
| 31 | アール さん | 2015/6/4 18:43 | |
| 32 | 石原ゼミ さん | 2015/6/5 14:55 | 兵庫県美方郡香美町 |
| 33 | sano_kuma さん | 2015/6/11 8:18 | 茨城県 |
| 34 | めざせ囲碁6段 さん | 2015/6/17 18:56 | 長野県小学校教諭 |
| 35 | ますた~ さん | 2015/6/26 21:26 |
こたえは、168 でした。