塃恾偺傛偆側丄捀妏俙偺妏搙偑俀侽搙偺擇摍曈嶰妏宍乮AB=AC乯偑偁傝傑偡丅
俛俠亖俛俤偵側傞傛偆偵丄曈俙俠忋偵俤揰傪偲傝丄
俠揰偐傜丄佢俛俠俢亖俆侽亱偵側傞傛偆偵曈俙俛忋偵俢揰傪偲傝傑偟偨丅
偙偺帪丄佢俤俢俠偺戝偒偝傪媮傔偰壓偝偄丅
丂乽崱寧偺栤戣乿丂戞侾俁夞丂乮暯惉侾俀擭侾侽寧乯
丂
亙侾丏昗弨栤戣亜
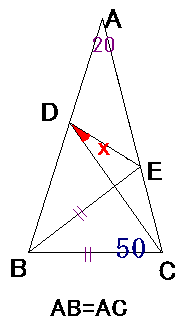
塃恾偺傛偆側丄捀妏俙偺妏搙偑俀侽搙偺擇摍曈嶰妏宍乮AB=AC乯偑偁傝傑偡丅 俛俠亖俛俤偵側傞傛偆偵丄曈俙俠忋偵俤揰傪偲傝丄 偙偺帪丄佢俤俢俠偺戝偒偝傪媮傔偰壓偝偄丅 |
 |
亙昗弨栤戣偺夝摎椺亜
仏仏仏rina偝傫偺夝摎仏仏仏仏仏仏仏
仮俙俛俠偼掙妏俉侽偺擇摍曈嶰妏宍
仮俛俠俢偱丂佢俠俛俢亖俉侽丂佢俛俠俢亖俆侽丂偐傜巆傝偺妏丂佢俛俢俠亖俆侽丂
廬偭偰丂仮俛俠俢偼丂丂俛俠亖俛俢丂偺擇摍曈嶰妏宍.............嘆
忦審傛傝丂丂俛俠亖俛俤............嘇
嘆嘇傛傝丂丂俛俠亖俛俤亖俛俢
偩偐傜揰俛偼丂仮俤俢俠偺奜愙墌偺拞怱偵側傞
屖俤俠偺拞怱妏丂佢俠俛俤亖俀侽丂丂傛偭偰丂屖俤俠偺墌廃妏丂佢俠俢俤亖侾侽
仏仏仏崅嫶丂摴峀丂偝傫偺夝摎仏仏仏仏仏
仏仏仏俴俬俷俶丂偝傫偺夝摎仏仏仏仏仏
梌偊傜傟偨妏搙偺忦審傛傝丄仮BEC偼BE亖BC側傞擇摍曈嶰妏宍丄仮BDC偼BD=BC側傞
擇摍曈嶰妏宍丅
丂傛偭偰丄BD=BE丅
丂妏DBE亖60搙偱偁傞偐傜丄妏EDC亖乮180搙亅60搙乯亐2亅妏BDC亖60搙亅50搙亖10搙丅
丂
丂
亙俀丏擄夝栤戣亜
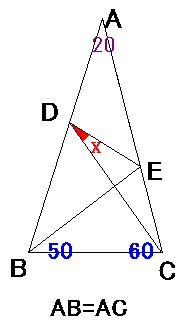
| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 塃恾偺傛偆側丄捀妏俙偺妏搙偑俀侽搙偺擇摍曈嶰妏宍乮AB=AC乯偑偁傝傑偡丅
偙偺帪丄佢俤俢俠偺戝偒偝傪媮傔偰壓偝偄丅 |
 |
亙擄夝栤戣偺夝摎椺亜
仏仏仏rina偝傫偺夝摎仏仏仏仏仏仏仏
昗弨栤戣偲摨條偵曈俙俛忋偵丂俠俛亖俠俥丂偲側傞揰俥傪偲傞
仮俥俠俢偱丂佢俛俠俥亖俀侽丂傛傝丂佢俥俠俢亖係侽丂佢俠俥俢亖侾俉侽亅俉侽亖侾
侽侽
偩偐傜巆傝偺妏丂佢俥俢俠亖係侽丂傛偭偰丂仮俥俠俢偼丂俥俠亖俥俢偺擇摍曈嶰妏宍
.......嘆
仮俠俛俤偱丂佢俛俠俤亖俉侽丂佢俠俛俤亖俆侽丂偩偐傜巆傝偺妏丂佢俠俤俛亖俆侽
傛偭偰丂仮俠俛俤偼丂俠俛亖俠俤偺擇摍曈嶰妏宍.............嘇
仮俠俤俥偱丂嘇傛傝丂俠俛亖俠俤丂丂傑偨丂俠俛亖俠俥丂偩偐傜丂俠俤亖俠俥
堦曽丂佢俤俠俥亖俉侽亅俀侽亖俇侽丂傛偭偰丂仮俠俤俥偼惓嶰妏宍
偡側傢偪丂俥俠亖俥俤...........嘊
嘆嘊傛傝丂俥俠亖俥俤亖俥俢
偩偐傜揰俥偼丂仮俤俢俠偺奜愙墌偺拞怱
屖俤俠偺拞怱妏丂佢俠俥俤亖俇侽丂乮惓嶰妏宍傛傝乯
傛偭偰屖俤俠偺墌廃妏丂佢俤俢俠亖俁侽
仏仏仏崅嫶丂摴峀丂偝傫偺夝摎仏仏仏仏仏
曈AB忋偵BC亖FC偲側傞揰F傪偲傝傑偡丅
仮俙BC偵偮偄偰丂妏ABC亖俉侽搙
仮BCF偵偮偄偰丂妏CFB亖妏FBC亖俉侽搙丂妏FCB亖俀侽搙
丂丂丂丂丂丂丂丂丂丂丂BC亖CF乧嘆
仮CDF偵偮偄偰丂妏CFD亖俇侽亅俀侽亖係侽
丂丂丂丂丂丂丂丂丂丂丂妏CDF亖係侽乮仮BCD偵拝栚乯
丂丂丂丂丂丂丂丂丂丂傛偭偰擇摍曈嶰妏宍偱偁傞偐傜丄FC亖FD乧嘇
仮BCE偵偮偄偰丂妏CBE亖妏BEC亖俆侽搙
丂丂丂丂丂丂丂丂丂丂傛偭偰擇摍曈嶰妏宍偱偁傞偐傜丄BC=CE乧嘊
仮CEF偵偮偄偰丂嘆偲嘊偐傜CF亖CE丂妏FCE亖俇侽傛傝
丂丂丂丂丂丂丂丂丂丂惓嶰妏宍偱偁傞偐傜CF=EF乧嘋
仮DEF偵偮偄偰丂嘇偲嘋偐傜EF亖FD偱偁傞偐傜擇摍曈嶰妏宍
丂丂丂丂丂丂丂丂丂妏DFE亖侾俉侽亅俉侽亅俇侽亖係侽
丂丂丂丂丂丂丂丂丂丂丂丂丂乮F偺傑傢傝偺妏偵拝栚乯
丂丂丂丂丂丂丂丂丂妏FEE亖乮侾俉侽亅係侽乯/俀亖俈侽
偙傟偐傜丄妏CDE亖妏FDE-妏FDC亖俈侽亅係侽亖俁侽
摎偊俁侽亱丂丂丂丂丂丂丂丂丂
仏仏仏俴俬俷俶丂偝傫偺夝摎仏仏仏仏仏
丂C偐傜AB忋偵妏FCB亖20搙偲側傞傛偆側揰F傪偲傞偲妏BFC=妏FBC=80搙偲側傞偐傜丄
CF=CB丅
丂傑偨丄梌偊傜傟偨忦審傛傝妏EBC=50搙丄妏C亖80搙偩偐傜妏BEC=50搙偲側傝丄CB=CE丅
丂偝傜偵丄妏ECF=80搙-20搙亖60搙偱偁傞偐傜丄仮EFC偼惓嶰妏宍丅傛偭偰丄FC=FE丅
丂師偵仮FCD偵拲栚偡傞偲丄妏BFC亖80搙丄妏DCF=40搙傛傝丄妏FDC=40搙丅
丂傛偭偰FD=FC丅
丂埲忋傛傝丄FD=FE偲側傞偐傜妏FDE=妏DEF丅
丂
丂妏EFD=180搙亅80搙亖60搙亖40搙傛傝丄
丂妏EDC=乮180搙亅40搙乯亐2亅妏FDC亖70搙亅40搙亖30搙丅