「今月の問題」 第195回 (平成27年12月)
<問題>
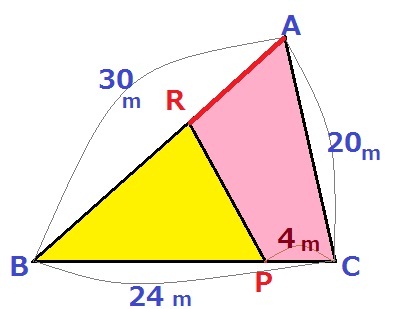
右図のように3辺の長さAB、BC、CAの長さがそれぞれ、30m、24m、20mの三角形ABCがあります。
線分PRは、三角形ABCの面積を2等分します。
ここで問題です。
PCの長さが4mの時、ARの長さは何mになるでしょうか。
|
 |
<正解者一覧表>
| 順位 |
name |
メール到着日時 |
備 考 |
| 1 |
源内シンガポール さん |
2015/12/1 0:03 |
長崎県 |
| 2 |
algebra さん |
2015/12/1 0:09 |
神奈川県 |
| 3 |
kou さん |
2015/12/1 0:09 |
さいたま |
| 4 |
バニラ さん |
2015/12/1 0:10 |
|
| 5 |
ゴンとも さん |
2015/12/1 0:32 |
豊川市 |
| 6 |
朝霞おじ さん |
2015/12/1 0:42 |
埼玉県 |
| 7 |
Mr.ダンディ さん |
2015/12/1 1:19 |
|
| 8 |
鯨鯢(Keigei) さん |
2015/12/1 5:39 |
|
| 9 |
いちもく さん |
2015/12/1 5:44 |
立川市 |
| 10 |
巷の夢 さん |
2015/12/1 5:50 |
神奈川県在住 |
| 11 |
ユートニウム さん |
2015/12/1 6:31 |
|
| 12 |
次郎長 さん |
2015/12/1 6:33 |
朝が寒い兵庫県 |
| 13 |
AKIRA さん |
2015/12/1 7:24 |
豊川市 |
| 14 |
佐野のくま さん |
2015/12/1 7:49 |
茨城県 |
| 15 |
やぶコウノトリ さん |
2015/12/1 8:39 |
兵庫県 |
| 16 |
いぬたこ さん |
2015/12/1 9:33 |
千葉県 |
| 17 |
織田ノブなが さん |
2015/12/1 9:33 |
愛知県 |
| 18 |
アール さん |
2015/12/1 13:33 |
|
| 19 |
うたねこ さん |
2015/12/1 14:14 |
東京 |
| 20 |
やまもとひさし さん |
2015/12/1 14:15 |
愛知県 |
| 21 |
マッキー27 さん |
2015/12/1 21:13 |
愛知県 |
| 22 |
朝霞お兄 さん |
2015/12/1 23:43 |
| 23 |
つねまる さん |
2015/12/2 13:20 |
千葉県 |
| 24 |
こころ さん |
2015/12/2 13:34 |
京都府 |
| 25 |
石原ゼミ さん |
2015/12/2 15:14 |
|
| 26 |
NNR4 さん |
2015/12/2 21:30 |
兵庫県 |
| 27 |
スモークマン さん |
2015/12/2 23:01 |
|
| 28 |
りーくん さん |
2015/12/2 23:03 |
埼玉県 |
| 29 |
たかひろ さん |
2015/12/3 2:34 |
埼玉県 |
| 30 |
男はつらいよ さん |
2015/12/3 9:46 |
神奈川県 |
| 31 |
GUTENTAG さん |
2015/12/3 12:10 |
滋賀県 |
| 32 |
あめい さん |
2015/12/3 16:40 |
|
| 33 |
PIN さん |
2015/12/3 18:49 |
|
| 34 |
保和 さん |
2015/12/4 5:32 |
尾張 |
| 35 |
新世界の神 さん |
2015/12/5 13:51 |
|
| 36 |
ぐっぴー さん |
2015/12/7 7:15 |
大阪府 |
| 37 |
めざせ囲碁6段 さん |
2015/12/8 16:31 |
長野県小学校教諭 |
| 38 |
いしぐろひろき さん |
2015/12/8 19:44 |
愛知県 |
| 39 |
KAZ さん |
2015/12/9 10:11 |
熊本県 |
| 40 |
yyyyy さん |
2015/12/10 16:25 |
|
| 41 |
でくのぼう さん |
2015/12/11 22:04 |
兵庫県 |
| 42 |
リンゴ さん |
2015/12/15 12:36 |
秋田県 |
| 43 |
??? さん |
2015/12/25 8:40 |
|
| 44 |
うさぎとかめ さん |
2015/12/31 20:48 |
福岡県 |
1
答えは12cmでした
[
133]
Re:[132] 俺小6何だけどこんなときかたでいいの? 投稿者:
巷の夢 <12gatu> 投稿日: 2015/12/13(Sun) 07:36
なる程、小学生はこの様に考えるのですね・・・・。
良いと思いますが、こう考えるとより簡単になりますね。
二つの⊿ABCと⊿RBPは∠Bが等しいので面積の比は
AB×BCとBR×BCとなります。この比は題意より2:1
なので、30×24/BR×20=2、因って、BR=18となる。
これよりAR=30-18=12である。
[
132]
俺小6何だけどこんなときかたでいいの? 投稿者:
新世界の神
<12gatu> 投稿日: 2015/12/05(Sat) 14:10
まず、△ABCと△BPRの面積の比を考えると文章から2:1とわかる。なのでそこからAB分のRB×BC分のBP=2分の1という式が成り立つ。なので逆算すると2分の1÷24分の20(6分の5)=10分の6と出る。この商の6は図の18㎝なので、18×6分の4(3分の2)の積12が答えとなる。
どうでしょうか。アドバイスよろしくお願いします。
[
131]
Re:[130] 来年は年間通して挑戦を・・・ 投稿者:
Mr.ダンディ <12gatu> 投稿日: 2015/12/03(Thu) 18:18
(Mr.ダンディさん、相変わらずスマート→ダンディですね)
いえいえ
あめいさん、次郎長さんの解法の方が「算数」らしくていいですね。
(私の計算式では、どちらかといえば「数学」かな?と思っていました。
吉岡先生、皆さま 本年も有り難うございました。
[
130]
来年は年間通して挑戦を・・・ 投稿者:
あめい <12gatu> 投稿日:
2015/12/03(Thu) 16:40
次郎長さんと同じように(分け方は違いましたが)
△ABP:△APC=5:1より
△PAR:△PRB=2:3=AR:RB
よってAR=30*2/5=12
と求めました。(Mr.ダンディさん、相変わらずスマート→ダンディですね)
他のサイトからたどり着いたこちらも、来年は年間通して挑戦させていただこうと思っています。
みなさんよろしくお願いします。
[
129]
もう12月なのねぇ…^^; 投稿者:
スモークマン <12gatu> 投稿日:
2015/12/02(Wed) 23:01
わたしゃ...18で送ってしまったかも…^^;
12月の問題だったから,そりゃ12でしたのね♪
[
128]
そうなんだ 投稿者:
次郎長 <12gatu> 投稿日:
2015/12/01(Tue) 10:58
Mr.ダンディさん、 巷の夢さんの解法。そうですね。
それが簡単でしたね。
今日はそっちに気づかずに
△BRP:△RPC=5:1
□ARPC=△BRCから、△ARC=5-1=4
つまり、AR:RB=4:6
AR=30*4/10=12と正式に?求めました。
この問題、好きです。来年も気楽に頑張ります
[
127]
どうなるかと思った 投稿者:
いぬたこ <12gatu>
投稿日: 2015/12/01(Tue) 09:30
三角形の高さをいろいろ変数で置き、どうにでもなれと数式を変形したら高さの変数が消えて答えが出た。
[
125]
12(月) 投稿者:
Mr.ダンディ <12gatu>
投稿日: 2015/12/01(Tue) 01:25
BR=a とすると
(20/24)*(a/30)=1/2 となり
a=18
AR=30-18=12
(AC=20 はカモフラージュですね)
[
124]
座標に 投稿者:
ゴンとも <12gatu> 投稿日:
2015/12/01(Tue) 00:30
B(0,0),C(24,0),P(20,0)とおき
点B,Cを中心にそれぞれ半径30,20の円の交点としてAを求め
直線BAの方程式が求まりRのx座標をaとおきBP*a*直線BAの傾き/2=BC*Aのy座標/4でaを求め
ARを三平方で求める XMaxima で
solve([x^2+y^2=30^2,(x-24)^2+y^2=20^2],[x,y])$
part(%,2)$rhs(part(%o2,1))$rhs(part(%o2,2))$
factor(%o4/%o3)$rhs(part(solve(%o5*a*10=6*%o4,a),1))$
sqrt((%o3-%o6)^2+(%o4-%o6*%o5)^2);12・・・・・・(答え)

