「今月の問題」 第196回 (平成28年1月)
<問題>
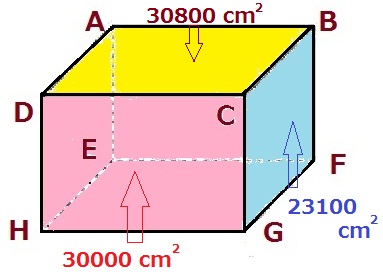
右図のような大きな直方体のABCD-EFGHがあります。頂点Cの3つの長方形の面積を求めたところ、上の面は30800cm2、左の面は30000cm2、左の面は23100cm2でした。
ここで問題です。この直方体には辺が12本ありますが、合計すると何cmになるでしょうか。
|
 |
<正解者一覧表>
| 順位 |
name |
メール到着日時 |
備 考 |
| 1 |
itsu さん |
2016/1/1 0:05 |
大阪府小6 |
| 2 |
源内シンガポール さん |
2016/1/1 0:07 |
長崎県 |
| 3 |
ゴンとも さん |
2016/1/1 0:10 |
豊川市 |
| 4 |
朝霞おじ さん |
2016/1/1 0:12 |
埼玉県 |
| 5 |
次郎長 さん |
2016/1/1 0:13 |
兵庫県 |
| 6 |
kou さん |
2016/1/1 0:13 |
さいたま |
| 7 |
algebra さん |
2016/1/1 0:15 |
神奈川県 |
| 8 |
男はつらいよ さん |
2016/1/1 0:16 |
神奈川県 |
| 9 |
マッキー27 さん |
2016/1/1 0:19 |
愛知県 |
| 10 |
バニラ さん |
2016/1/1 0:22 |
|
| 11 |
teki さん |
2016/1/1 0:55 |
大阪府 |
| 12 |
佐野のくま さん |
2016/1/1 2:17 |
茨城県 |
| 13 |
デアルケ さん |
2016/1/1 3:21 |
三重県紀北町 |
| 14 |
いちもく さん |
2016/1/1 6:51 |
立川市 |
| 15 |
巷の夢 さん |
2016/1/1 7:13 |
神奈川県在住 |
| 16 |
アール さん |
2016/1/1 7:49 |
|
| 17 |
まいすた さん |
2016/1/1 9:58 |
|
| 18 |
AKIRA さん |
2016/1/1 10:41 |
豊川市 |
| 19 |
GUTENTAG さん |
2016/1/1 12:12 |
滋賀県 |
| 20 |
スモークマン さん |
2016/1/1 12:20 |
@新倉敷 |
| 21 |
石原ゼミ さん |
2016/1/1 13:04 |
|
| 22 |
uchinyan さん |
2016/1/1 15:31 |
|
| 23 |
鯨鯢(Keigei) さん |
2016/1/1 16:08 |
|
| 24 |
ユートニウム さん |
2016/1/1 19:53 |
|
| 25 |
Mr.ダンディ さん |
2016/1/1 21:58 |
大阪府 |
| 26 |
めざせ囲碁6段 さん |
2016/1/2 10:07 |
長野県小学校教諭 |
| 27 |
りーくん さん |
2016/1/2 18:08 |
埼玉県 |
| 28 |
寺脇 犬 さん |
2016/1/2 23:32 |
生駒市 |
| 29 |
虹パパ さん |
2016/1/4 8:45 |
東京都 |
| 30 |
KAZ さん |
2016/1/4 12:57 |
熊本県 |
| 31 |
つねまる さん |
2016/1/6 15:45 |
千葉県 |
| 32 |
やぶコウノトリ さん |
2016/1/6 16:58 |
兵庫県 |
| 33 |
??? さん |
2016/1/7 8:32 |
|
| 34 |
でくのぼう さん |
2016/1/7 19:37 |
兵庫県 |
| 35 |
カルダノ さん |
2016/1/7 19:55 |
群馬県 |
| 36 |
いぬたこ さん |
2016/1/8 15:54 |
千葉県 |
| 37 |
保和 さん |
2016/1/8 15:55 |
愛知県 |
| 38 |
yss さん |
2016/1/8 16:00 |
東京都 |
| 39 |
うたねこ さん |
2016/1/9 4:42 |
東京 |
| 40 |
うさぎとかめ さん |
2016/1/9 13:31 |
福岡県 |
| 41 |
しぐま さん |
2016/1/31 18:49 |
神奈川県 高校生 |
答えは2016cmでした。皆さんの解答ありがとうございました。
[
144]
こんなやり方もあり? 投稿者:
くろ <1gatu>
投稿日: 2016/01/29(Fri) 14:00
CG:CB=300:308
試しに300*308を計算すると92400
これがちょうど23100の4倍
てことは300と308を半分にして
CGが150、CBが154と分かります
ここまでできればあとは説明いりませんね
[
143]
できた 投稿者:
いぬたこ <1gatu> 投稿日:
2016/01/08(Fri) 15:52
代数でx、y、zとしてやってしまった。
うまい方法あるのかな?
[
142]
美しい問題ですね。 投稿者:
あめい <1gatu> 投稿日:
2016/01/06(Wed) 13:53
みなさんと同じですが、2.3.5.7.11ときれいに素数が並んだ数になるのですね。
美しい!
[
141]
電卓で すみませんね。 投稿者:
お久し振りです。
<1gatu> 投稿日: 2016/01/03(Sun) 16:58
頂点Cからの三辺を x,y,z,とすると
x^2・y^2・z^2=21344400000000 より
xyz=
4620000で
三辺は 200 154 150
各々を四倍して 2016
[
140]
おめでとうございます。 投稿者:
Mr.ダンディ
<1gatu> 投稿日: 2016/01/01(Fri) 22:11
昨日は忘れており遅れての回答です。
ab=2^2*7*11*100 .............①
bc=3*7*11*100 ..............②
ca=2^2*3*5^2 ...............③
①*②*③より
(abc)^2=(2^4)*(3^)2*(5^2)*(7^2)*(11^2)*10^6
abc=(2^2)*3*5*7*11*1000 ..........④
④÷②、④÷③、④÷① より
a=200
,b=154 ,c=150
求める値=4*(200+154+150)=2016
と求めました。
本年もよろしくお願いいたします。
[
139]
あけましておめでとうございます☆ 投稿者:
スモークマン <1gatu> 投稿日:
2016/01/01(Fri) 12:19
ab=308(00)
ac=231(00)
bc=300(00)
308=2^2*77
231=3*77
300=3*10^2
abc=2*3*10*77
c=3*10/2
b=2*10
a=2*77/10
それぞれ 10倍して、
a=154, b=200, c=150
4(a+b+c)=4(154+200+150)=4*504=2016♪
今年もよろしくお願いしま~す~m(_ _)m~☆
[
138]
明けましておめでとうございます 投稿者:
まいすた
<1gatu> 投稿日: 2016/01/01(Fri) 09:55
b≡CB,d≡CD,g≡CGと定義します。
(b+d+g)^2=b^2+d^2+g^2+2(bd+dg+gb)
b^2=gb・bd/dg
d^2,g^2:以下同様
bd=30800
dg,gb:以下同様
(b+d+g)^2=254016
よって、
4(b+d+g)=2016
http://primzahl.seesaa.net/
[
137]
新年おめでとうございます 投稿者:
次郎長
<1gatu> 投稿日: 2016/01/01(Fri) 08:30
吉岡先生、今年もよろしくお願いします。
私は電卓を使いましたが、使い慣れていない電卓だったもので、
おかしな数字が出てきて新年早々、誤答を2回も送ってしまいました。
自信満々に誤答を送る。これも楽しきかな。ん?
[
136]
2016年が来ましたね・・・ 投稿者:
巷の夢
<1gatu> 投稿日: 2016/01/01(Fri) 07:18
吉岡先生、2016年も毎月面白い問題を宜しくお願い申し上げます。
ゴンとも様と同じ解法ですが、手計算で・・・。
[
135]
あけましておめでとうございます 投稿者:
佐野のくまさん
<1gatu> 投稿日: 2016/01/01(Fri) 02:19
年明けから苦労しました。
毎回楽しませてもらっています。
今年も宜しくお願いします。
[
134]
明けましておめでとうございます。 投稿者:
ゴンとも
<1gatu> 投稿日: 2016/01/01(Fri) 01:25
AB=CD=GH=FE=a,BC=FG=EH=AD=b,CG=BF=DH=AE=cとして以下の3方程式が立ちそれを
連立方程式として XMaxima で解くと
part(solve([4*(a+b+c)=x,a*b=30800,c*a=30000,b*c=23100],[a,b,c,x]),2);
a=200,b=154,c=150,x=2016・・・・・・(答え)
今年の西暦が答えでしたね。今年もよろしくお願いします。

