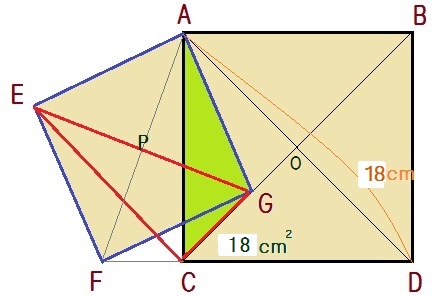
右図のように、対角線の長さが18cmの正方形ABCDがあります。この対角線BC上に三角形AGCの面積が18cm2になるように点Gを取ります。
そして、AGを一辺とする正方形AEFGを作ります。
ここで問題です。三角形ECGの面積は何cm2になるでしょうか。
|
<問題> 右図のように、対角線の長さが18cmの正方形ABCDがあります。この対角線BC上に三角形AGCの面積が18cm2になるように点Gを取ります。 そして、AGを一辺とする正方形AEFGを作ります。 ここで問題です。三角形ECGの面積は何cm2になるでしょうか。 |
 |
<正解者一覧表>
| 順位 | name | メール到着日時 | 備 考 |
| 1 | AKIRA さん | 2016/2/1 0:16 | 豊川市 |
| 2 | 源内シンガポール さん | 2016/2/1 0:17 | 長崎県 |
| 3 | バニラ さん | 2016/2/1 0:25 | |
| 4 | Mr.ダンディ さん | 2016/2/1 0:26 | |
| 5 | algebra さん | 2016/2/1 0:27 | 神奈川県 |
| 6 | ゴンとも さん | 2016/2/1 0:28 | 豊川市 |
| 7 | 男はつらいよ さん | 2016/2/1 0:29 | 神奈川県 |
| 8 | kou さん | 2016/2/1 0:31 | さいたま |
| 9 | 寺脇犬 さん | 2016/2/1 1:05 | 生駒市 |
| 10 | 鯨鯢(Keigei) さん | 2016/2/1 5:27 | |
| 11 | ユートニウム さん | 2016/2/1 6:29 | |
| 12 | 朝霞おじ さん | 2016/2/1 6:43 | 埼玉県 |
| 13 | 次郎長 さん | 2016/2/1 7:47 | 少し暖かくなった兵庫県 |
| 14 | いちもく さん | 2016/2/1 11:01 | 立川市 |
| 15 | uchinyan さん | 2016/2/1 14:02 | 東京都 |
| 16 | 岡本ボンバーズ さん | 2016/2/1 14:29 | 秋田県 |
| 17 | やぶコウノトリ さん | 2016/2/1 14:38 | 兵庫県 |
| 18 | 初芝立命館高校 さん | 2016/2/1 17:02 | 3年4組 |
| 19 | マッキー27 さん | 2016/2/1 20:09 | 愛知県 |
| 20 | teki さん | 2016/2/1 21:09 | 大阪府 |
| 21 | スモークマン さん | 2016/2/1 23:10 | @新倉敷 |
| 22 | 巷の夢 さん | 2016/2/2 7:24 | @新倉敷 |
| 23 | いぬたこ さん | 2016/2/2 9:11 | 千葉県 |
| 24 | うたねこ さん | 2016/2/2 9:30 | 東京 |
| 25 | 保和 さん | 2016/2/2 9:48 | 尾張 |
| 26 | GUTENTAG さん | 2016/2/2 9:54 | 滋賀県 |
| 27 | itsu さん | 2016/2/2 16:30 | 大阪府小6 |
| 28 | まいすた さん | 2016/2/3 0:03 | |
| 29 | べんべん さん | 2016/2/3 4:09 | 埼玉県 |
| 30 | デアルケ さん | 2016/2/3 9:00 | 紀北町 |
| 31 | 佐野のくま さん | 2016/2/3 11:05 | 茨城県 |
| 32 | NNR4 さん | 2016/2/3 21:38 | 兵庫県 |
| 33 | あめい さん | 2016/2/4 17:35 | |
| 34 | りーくん さん | 2016/2/6 21:18 | 埼玉県 |
| 35 | うさぎとかめ さん | 2016/2/6 22:17 | 埼玉県 |
| 36 | 石原ゼミ さん | 2016/2/7 16:54 | |
| 37 | たかひろ さん | 2016/2/10 0:41 | 埼玉県 |
| 38 | アール さん | 2016/2/13 17:21 | |
| 39 | ねねね さん | 2016/2/15 20:30 | 兵庫県三木市 |
| 40 | めざせ さん | 2016/2/16 21:29 | 長野県小学校 |
答えは、28cm2でした。