「今月の問題」 第202回 (平成28年7月)
(今月は、右図の小学校5年生の算数教科書問題に挑戦して下さい。)
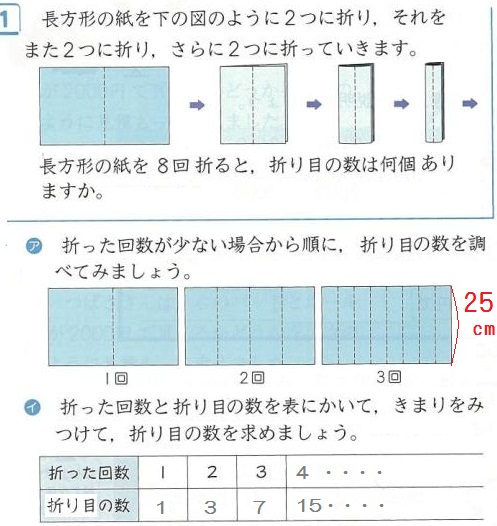
長方形の紙を2つ折りに、繰り返し折っていきます。次の問題に答えて下さい。
<問題1>
長方形の紙を2つに折っていくと、折り目の数は1本、3本、7本・・・と増えます。8回折ると、折り目の数は何本になりますか。
<問題2>
長方形の縦は25cmとします。折り目の長さの和を考えると、1回では25cm、2回では75cm、3回では175cmになります。折り目の長さの和が1000mを超えるのは何回折った時でしょうか。
※実際に、授業で大きな紙を折る活動を見ましたが、6回ぐらいで限界でした。
 |
 |
<正解者一覧表>
| 順位 |
name |
メール到着日時 |
備 考 |
| 1 |
teki さん |
2016/7/1 0:05 |
大阪府 |
| 2 |
algebra さん |
2016/7/1 0:07 |
神奈川県 |
| 3 |
kou さん |
2016/7/1 0:11 |
さいたま |
| 4 |
GOGOGIANTS さん |
2016/7/1 0:12 |
|
| 5 |
Mr.ダンディ さん |
2016/7/1 0:16 |
|
| 6 |
バニラ さん |
2016/7/1 0:23 |
|
| 7 |
ゴンとも さん |
2016/7/1 0:25 |
豊川市 |
| 8 |
デアルケ さん |
2016/7/1 2:21 |
三重県紀北町 |
| 9 |
巷の夢 さん |
2016/7/1 5:40 |
神奈川県在住 |
| 10 |
朝霞おじ さん |
2016/7/1 5:57 |
埼玉県 |
| 11 |
次郎長 さん |
2016/7/1 6:02 |
暑い夏が来るそうな、兵庫県 |
| 12 |
いちもく さん |
2016/7/1 8:10 |
立川市 |
| 13 |
いぬたこ さん |
2016/7/1 10:54 |
千葉県 |
| 15 |
うたねこ さん |
2016/7/1 10:55 |
東京 |
| 16 |
保和 さん |
2016/7/1 10:56 |
愛知県 |
| 17 |
uchinyan さん |
2016/7/1 10:58 |
東京都 |
| 18 |
アオリイカ さん |
2016/7/1 14:08 |
愛知県 |
| 19 |
NNR4 さん |
2016/7/1 20:24 |
兵庫県 |
| 20 |
カルダノ さん |
2016/7/1 21:25 |
群馬 |
| 21 |
ユートニウム さん |
2016/7/1 21:38 |
|
| 22 |
鯨鯢(Keigei) さん |
2016/7/1 22:48 |
|
| 23 |
アール さん |
2016/7/2 9:02
|
|
| 24 |
うさぎとかめ さん |
2016/7/2 12:03
|
|
| 25 |
たかひろ さん |
2016/7/3 14:21
|
|
| 26 |
りーくん さん |
2016/7/4 20:12 |
埼玉県 |
| 27 |
まいすた さん |
2016/7/4 23:27 |
|
| 28 |
石原ゼミん さん |
2016/7/4 23:59 |
|
| 29 |
ローリー さん |
2016/7/5 9:48 |
大阪府 |
| 30 |
dyslexia さん |
2016/7/5 15:57 |
大阪府 |
| 31 |
スモークマン さん |
2016/7/5 18:34 |
@新倉敷 |
| 32 |
JUST_COMMUNICATION さん |
2016/7/6 19:15 |
|
| 33 |
やぶコウノトリ さん |
2016/7/7 9:32 |
|
| 34 |
hiroki さん |
2016/7/8 13:21 |
東京都 |
| 35 |
男はつらいよ さん |
2016/7/14 14:04 |
神奈川県 |
| 36 |
そんなの関係ねえ さん |
2016/7/14 14:10 |
|
| 37 |
コーセージ さん |
2016/7/19 23:15 |
大阪府枚方 |
答えは、255本と12回でした。
[
222]
小学生の問題なのねぇ ^^; 投稿者:
スモークマン <15> 投稿日:
2016/07/05(Tue) 14:26
こんなのが小学生の問題なんですのねぇ ^^;
わたしん時はこういうのなかったような…?
1+2+2^2+…+2^8=2^9-1=511
1024*2<4000<1024*4=2^12
色んなバージョンが考えられますね☆
[
221]
12回折れるものは? 投稿者:
まいすた <15>
投稿日: 2016/07/04(Mon) 23:26
太陽帆船イカロスのソーラーセイル(厚さ7.5μm,幅14m)なら12回ぐらい折れるかなと思ったのですが、全然無理そうでした。
幅が100mの金箔(厚さ0.1μm)なら12回折れそうです。
12回折ると、単純計算で厚さ約0.41mm、幅約24mmになります。
最後の方は折り曲げる時の層間摩擦がとんでもないことになるので、破らずに折るのは大変ですが。
http://primzahl.seesaa.net/
[
220]
Re:[218] 紙の厚みを考えれば、12回も折ることは不可能です
投稿者:
teki <15> 投稿日:
2016/07/01(Fri) 23:41
>
勿論、折り目の数は、2^nー1より考えるのですが、表から階差数列で考えることもできます。
教科書では、明らかに階差数列(規則性)を意識させるのが目的な表記になっていますが、実は折ってできる面の数を考えれば、折り目の数は簡単に出てきます。
n回折ると、できる面の数は明らかに2^nですので、折り目を面と面の境界線と捉えれば、その数は2^n-1です。
そういう意味では、階差数列の例示としては不適切かもしれませんね。
算数・数学の専門家でない私が言うのも、どうかと思いますが、ちょっと気になったもので・・・。
[
219]
折り目の幅を考えれば 投稿者:
鯨鯢(Keigei)
<15> 投稿日: 2016/07/01(Fri) 22:58
まず私は、折り目が25cmから1000mと4000倍になれば、折り目の幅が1/4001になるので、
紙の横の長さが40cmあっても、0.1mm未満の幅の折り目なんて無理だと思いました。
もちろん、その後で真面目に解きました。
[
218]
紙の厚みを考えれば、12回も折ることは不可能です 投稿者:
よしおか <15> 投稿日: 2016/07/01(Fri) 16:42
今回の問題は、啓林館の5年生の教科書問題を出題しました。
勿論、折り目の数は、2^nー1より考えるのですが、表から階差数列で考えることもできます。
算数数学が、積み上げの教科であるあることを実感させることができるように思います。
ところで、tekiさんの書かれているように、厚みを考えると12回も折ることができないことが分かりますが、わずか12回折り曲げることにより厚みが41cmになったり、折り目の長さの和が1000mを越えること示したいと思いました。
[
217]
↓ すんません。桁を間違えました。 投稿者:
teki <15> 投稿日: 2016/07/01(Fri)
15:15
0.1mmの厚さの紙を12回折れば、その厚みは約41cmです。
[
216]
Re:[215] ひっかかりました・・・ 投稿者:
teki <15> 投稿日: 2016/07/01(Fri)
15:11
> >
An=2^n-1が出たので、1000cmは6回で・・・・、えーえー入れない、
> >
何故、問題をよく見ると、1000mでした。悪い癖が・・・、とほほ
> > でした。
>
> 全く同様のことをしていました。
> (引っかかるのが普通かも・・と開き直る私)
確かに常識的に考えれば、12回も折るのはほとんど不可能に近いですものね。
仮に0.1mmの厚さの紙を12回折れば、その厚みは4mを超えることになります。
実際には、間に隙間ができるので、もっと厚くなりますね。
問題のページでも書かれているとおり、実験しようとしても6~7回が限界のようです。
[
215]
Re:[213] ひっかかりました・・・ 投稿者:
Mr.ダンディ <15> 投稿日: 2016/07/01(Fri) 14:18
>
An=2^n-1が出たので、1000cmは6回で・・・・、えーえー入れない、
> 何故、問題をよく見ると、1000mでした。悪い癖が・・・、とほほ
> でした。
全く同様のことをしていました。
(引っかかるのが普通かも・・と開き直る私)
[
214]
すっきり 投稿者:
いぬたこ <15> 投稿日:
2016/07/01(Fri) 10:52
最初めんどくさく感じたが意外とすっきり解けました。
[
213]
ひっかかりました・・・ 投稿者:
巷の夢 <15>
投稿日: 2016/07/01(Fri) 05:49
An=2^n-1が出たので、1000cmは6回で・・・・、えーえー入れない、
何故、問題をよく見ると、1000mでした。悪い癖が・・・、とほほ
でした
問題1は、2^8-1=255本
問題2は、2^12-1=4095 で、4095×0.25=1023.75の時。
久しぶりのリアルタイム参加です。

