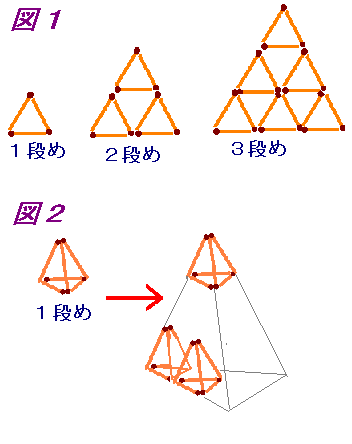
長さの同じマッチ棒が１，０００本あります。 図１のようにマッチ棒で正三角形を作っていきます。 例えば、１段めは３本、２段めを作る時は、９本のマッチ棒が必要です。 ＜問題１＞１０００本のマッチでは、何段重ねることができるでしょうか。 ＜問題２＞また、図２のように立体に応用し、正四面体を作ってみます。 　　　　　　　１０００本のマッチ棒では、何段重ねることができるでしょうか。 　 （※もちろん、１０００本のマッチ棒のうち、幾本かは使わない。）

＜解答例＞
＊＊＊高橋 道広さんの解答＊＊＊＊＊＊＊
（１）水平なマッチは全体の1/3だから
全体は、(1+2+3+...+n)*3=3n(n+1)/2　　n=25のとき975
n=26のとき　1053　より２５
（２）水平面のマッチの数は、Σ3k(K+1)/2=n(n+1)(n+2)/2
４つの面があり、それぞれのマッチは2回数えられているので
マッチの総数はこの４倍の半分つまりn(n+1)(n+2)になる
n=9のとき990　n=10のとき1320より　９

＊＊＊浜田　明巳さんの解答＊＊＊＊＊＊＊
　問題１においては，段数をｎ，最下段の三角形の数をａ(ｎ)とすると，
　　ａ(ｎ)＝ｎ
となります．
　このａ(ｎ)を使い，
　　３Σ(1≦k≦n)ａ(ｋ)≦１０００＜３Σ(1≦k≦n+1)ａ(ｋ)
となるｎを求めればよいことが分かります．
　問題２においては，さらに最下段の四面体の数をｂ(ｎ)とすると，漸化式
　　ｂ(ｎ＋１)＝ｂ(ｎ)＋ａ(ｎ＋１)，ｂ(０)＝０
が成立します．
　このｂ(ｎ)を使い，
　　６Σ(1≦k≦n)ｂ(ｋ)≦１０００＜６Σ(1≦k≦n+1)ｂ(ｋ)
となるｎを求めればよいことが分かります．
　ＨＳＰはどちらかというと，ゲーム専用のソフトですが，整数計算だけでよければ，数学の問題を解くことができます．

ＵＢＡＳＩＣ
   10   'asave "0011.ub"
   20   dim A(100),B(100):N=1000
   30   Wa1=0:Kotae1=0
   40   while Wa1<=N
   50    A(Kotae1+1)=Kotae1+1
   60    Wa1+=3*A(Kotae1+1)
   70    if Wa1<=N then Kotae1+=1:print Wa1;
   80   wend
   90   print "->";Kotae1
  100   Wa2=0:Kotae2=0:B(0)=0
  110   while Wa2<=N
  120    B(Kotae2+1)=B(Kotae2)+A(Kotae2+1)
  130    Wa2+=6*B(Kotae2+1)
  140    if Wa2<=N then Kotae2+=1:print Wa2;
  150   wend
  160   print "->";Kotae2:end


ＨＳＰ（Ｈｏｔ　Ｓｏｕｐ　Ｐｒｏｃｅｓｓｏｒ）
; 0011.as
cls
mes "平成１２年１１月第１４回"
button "問題１", *start1
button "問題２", *start2
button "終了", *ending
stop
;
*start1
n=1000
wa=0
kotae=0
*kurikaeshi1
wa=3*(kotae+1)+wa
if wa<=n : kotae+=1 : goto *kurikaeshi1
mes "問題１："+kotae
stop
;
*start2
n=1000
a=0
b=0
wa=0
kotae=0
*kurikaeshi2
a+=1
b+=a
wa=6*b+wa
if wa<=n : kotae+=1 : goto *kurikaeshi2
mes "問題２："+kotae
stop
;
*ending
end

＊＊＊畠山さん、ＬＩＯＮさん　他の解答＊＊＊＊＊＊＊
<問題1の答え>

 n段目を作るのに必要な三角形の個数はn個
 したがって必要なマッチの本数は3n本
 よって
 Σ_{i=1}^{n}(3i) <= 1000  (*)
 を満たす最大のnを求めればよい。
 (*)の左辺は
 3n(n+1)/2
 である。これより(*)を満たす最大のnは25である。
 よって25段重ねることができる。

<問題2の答え>

n段目を作るのに必要な正四面体の個数はΣ_{i=1}^{n}(i)=n(n+1)/2個
したがって必要なマッチの本数は6n(n+1)/2=(3n^2+3n)本
よって
Σ_{i=1}^{n}(3n^2+3) <= 1000  (#)
を満たす最大のnを求めればよい。
(#)の左辺は
3n(n+1)(2n+1)/6+3n(n+1)/2=n(n+1)(n+2)
である。これより(#)を満たす最大のnは9である。
よって9段重ねることができる。