「今月の問題」　第２０３回　（平成２８年８月）
 
＜問題＞

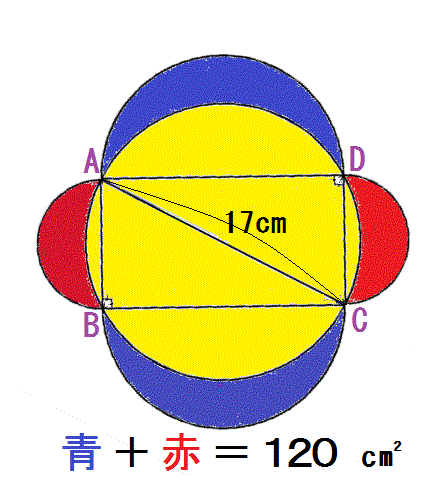
右図を見て下さい。四角形ABCDは、対角線が17cmの長方形です。
青色の三日月形はAD，BCを直径とする半円の一部です。
また、赤色の三日月形はAB，DCを直径とする半円の一部です。
黄色は直径が17cmの円です。
赤色の三日月形2つと青色の三日月形２つの面積の和は、120cm2であることが分かっています。


ここで問題です。
正方形の横ADと縦ABの長さは、それぞれ何cmでしょうか。
ただし、横は縦より長いと考えて下さい。

 

 

 ＜正解者一覧表＞　 　　　　　　　　　　　　　　　　　　　　
順位 　　　　ｎａｍｅ　　　 　　メール到着日時 　　 　　備　考　　
　１ algebra　さん 2016/8/1　0:14 神奈川県　
　２ 源内シンガポール　さん 2016/8/1　0:15 長崎県　
　３ 男はつらいよ　さん 2016/8/1　0:17 神奈川県　
　４ Ｍｒ．ダンディ　さん 2016/8/1　0:22 大阪府　
　５ バニラ　さん 2016/8/1　0:24 　
　６ kou　さん 2016/8/1　0:29 さいたま　
　７ 朝霞おじ　さん 2016/8/1　0:39 埼玉県　
　８ デアルケ　さん 2016/8/1　0:41 三重県紀北町　
　９ JUST_COMMUNICATION　さん 2016/8/1　2:46 　
１０ 巷の夢　さん 2016/8/1　3:10 神奈川県在住　
１１ ゴンとも　さん 2016/8/1　5:10 豊川市　
１２ 鯨鯢(Keigei)　さん 2016/8/1　7:43 　
１３ 次郎長　さん 2016/8/1　8:36 暑い暑い兵庫県　
１４ いぬたこ　さん 2016/8/1　8:46 千葉県　
１５ うたねこ　さん 2016/8/1　8:46 東京　
１６ 保和　さん 2016/8/1　9:04 愛知　
１７ やぶｺｳﾉﾄﾘ　さん 2016/8/1　11:11 兵庫県　
１８ uchinyan　さん 2016/8/1　12:00 東京都　
１９ GUTENTAG　さん 2016/8/1　13:56 滋賀県　
２０ teki　さん 2016/8/1　14:43 大阪府　
２１ dyslexia　さん 2016/8/1　17:24 大阪府　
２２ いちもく　さん 2016/8/1　17:54 立川市　
２３ りーくん　さん 2016/8/1　20:28 埼玉県　
２４ マッキー２７　さん 2016/8/1　21:23 愛知県　
２５ ユートニウム　さん 2016/8/1　22:30 　
２６ NNR4　さん 2016/8/1　22:42 兵庫県　
２７ 安倍しんぞう　さん 2016/8/2　3:34 とうきょう　
２８ AKIR　さん 2016/8/2　12:08 愛知県　
２９ フリードン　さん 2016/8/2　18:53 長野県　
３０ こいさぶろう　さん 2016/8/3　5:05 神奈川　
３１ ひも　さん 2016/8/3　9:47 兵庫県　
３２ 暑いです・８月　さん 2016/8/3　16:48 　
３３ まいすた　さん 2016/8/3　22:18 　
３４ ｙｙｙｙｙ　さん 2016/8/4　14:27 　
３５ 虹パパ　さん 2016/8/4　17:33 東京都　
３６ たかひろ　さん 2016/8/4　23:16 　
３７ ローリー　さん 2016/8/5　11:00 大阪府　
３８ 佐野のくま　さん 2016/8/13　10:24 茨城県　
３９ スモークマン　さん 2016/8/13　22:41 ＠新倉敷　
４０ 阿修羅　さん 2016/8/15　11:29 長野県小学校教諭　
４１ 石原ゼミ　さん 2016/8/22　8:18 　
４２ あめい　さん 2016/8/26　1:29 　

 

答えは、15ｃｍと8ｃｍでした。

 

[229] Re:[228] 長方形の対角線が 17だと 投稿者： teki <15> 投稿日： 2016/08/01(Mon) 22:35  
> これは ヒポクラテスの三日月を 倍にしたものですね。
>
> ところで 整数比の 直角三角形は ほかに
> 5 : 12 : 13 とか 7 : 24 : 25 とかが よく知られていますね

一番有名なのは、やはり３：４：５でしょうね。
なお、「ヒポクラテスの三日月」については、既にこのサイトの第１４５問で出題されていますね。
[228] 長方形の対角線が 17だと 投稿者： dyslexia <15> 投稿日： 2016/08/01(Mon) 17:18  
三辺が整数比の 直角三角形は 8,15,17だと 解ってしまいました。
8×15=120

これは ヒポクラテスの三日月を 倍にしたものですね。

ところで 整数比の 直角三角形は ほかに
5 : 12 : 13 とか 7 : 24 : 25 とかが よく知られていますね
[227] ヒポクラテスの三日月 投稿者： teki <15> 投稿日： 2016/08/01(Mon) 14:49  
ですよね。
着色部の面積＝長方形の面積なので、縦、横をａ、ｂとし、連立方程式

ａ×ｂ＝１２０
ａ＾２＋ｂ＾２＝２８９

を解いて、ａ＝８、ｂ＝１５
[226] 直観の方が早い 投稿者： 次郎長 <15> 投稿日： 2016/08/01(Mon) 09:06  
17㎝を見たときに、2辺は8㎝と15㎝と思いましたが、まぁ、計算してみようと・・・大変でした。
苦労しました。見た目よりもずいぶんと時間がかかりました。
[225] πが消えた 投稿者： いぬたこ <15> 投稿日： 2016/08/01(Mon) 08:44  
πの処分が不安だったが、消えてよかった。
[224] なんとか 投稿者： JUST_COMMUNICATION <15> 投稿日： 2016/08/01(Mon) 02:49  
ヒポクラテスの三日月＋三平方の定理で解きました。
[223] どうしても三平方の定理を使うことに・・ 投稿者： Ｍｒ．ダンディ <15> 投稿日： 2016/08/01(Mon) 00:43  
∠ＡＤＣ＝90°より
(ADを直径とする半円の面積)＋(CDを直径とする半円の面積)
＝(ACを直径とする半円の面積)
周囲の４つの半円の和＝ACを直径とする円

長方形ＡＢＣＤ＋周囲の４つの半円－ACを直径とする半円＝色のついた部分
だから
長方形ＡＢＣＤ＝120

AD=a,AB=b とすると
ab＝120 ・・・・・①
a^2+b^2＝17^2
より
a+b=√(17^2+120*2)＝23　・・・・・②
①②を満たすa,bは　15と 8

と求めました。