「今月の問題」 第205回 (平成28年10月)
<問題>
今回は、下図の算額の問題を数値を変えて出題します。
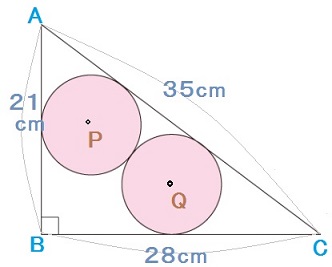
今、右図のように高さが21cm、底辺が28cm、斜辺の長さが35cmの直角三角形があります。その内部に,図のように、直径が等しい円Pと円Qを内接して書き入れます。
ここで問題です。
円の直径は何cmになるでしょうか。
|
 |
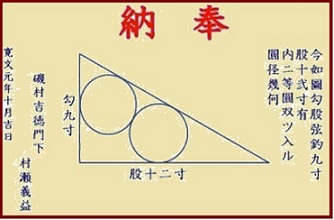
※ 算額とは、江戸時代、額や絵馬に数学の問題や解法を記して、神社や仏閣に奉納したものです。数学者のみならず、一般の数学愛好家が数多く奉納されています。内容のほとんどがユークリッド幾何学の分野の問題ですが、レベルは西欧の数学より何年も早く高度な定理を扱っていたものも少なくないとのことです。
右図は、渋谷・金王八幡神社に奉納された算額です。この問題は、直角三角形のの中にある同じ大きさの円の直径の長さを求めるものです。算額の問題としては比較的平易なものであると紹介してありましたが、私にとっては知的好奇心を満足させてくれる骨のある問題です。皆さんにとってはどうでしょうか。
|
 |
<正解者一覧表>
| 順位 |
name |
メール到着日時 |
備 考 |
| 1 |
teki さん |
2015/10/1 0:01 |
大阪府 |
| 2 |
ゴンとも さん |
2015/10/1 0:02 |
豊川市 |
| 3 |
algebra さん |
2015/10/1 0:03 |
神奈川県 |
| 4 |
kou さん |
2015/10/1 0:06 |
さいたま |
| 7 |
源内シンガポール さん |
2015/10/1 0:08 |
長崎県 |
| 8 |
男はつらいよ さん |
2015/10/1 0:09 |
神奈川県 |
| 9 |
デアルケ さん |
2015/10/1 0:14 |
三重県紀北町 |
| 10 |
バニラ さん |
2015/10/1 0:19 |
|
| 11 |
dyslexia さん |
2015/10/1 0:23 |
大阪府 |
| 12 |
マッキー27 さん |
2015/10/1 0:25 |
愛知県 |
| 13 |
ユートニウム さん |
2015/10/1 0:31 |
|
| 14 |
朝霞おじ さん |
2015/10/1 0:59 |
埼玉県 |
| 15 |
巷の夢 さん |
2015/10/1 5:34 |
神奈川県在住 |
| 16 |
いちもく さん |
2015/10/1 9:00 |
立川市 |
| 17 |
まいすた さん |
2015/10/1 10:17 |
|
| 18 |
次郎長 さん |
2015/10/1 11:03 |
兵庫県 |
| 19 |
uchinyan さん |
2015/10/1 13:16 |
|
| 20 |
りーくん さん |
2015/10/1 21:36 |
埼玉県 |
| 21 |
NNR4 さん |
2015/10/2 11:00 |
兵庫県 |
| 22 |
阿修羅 さん |
2015/10/2 17:21 |
長野県小学校教諭 |
| 23 |
鯨鯢(Keigei) さん |
2015/10/2 19:30 |
|
| 23 |
GUTENTAG さん |
2015/10/3 10:14 |
滋賀県 |
| 24 |
いぬたこ さん |
2015/10/3 14:47 |
千葉県 |
| 25 |
うたねこ さん |
2015/10/3 14:19 |
東京 |
| 26 |
保和 さん |
2015/10/3 15:26 |
愛知 |
| 27 |
たかひろ さん |
2015/10/3 21:41 |
埼玉県 |
| 28 |
Mr.ダンディ さん |
2015/10/4 8:41 |
|
| 29 |
マリアシャチホコ さん |
2015/10/4 13:43 |
ロシア |
| 30 |
やぶコウノトリ さん |
2015/10/4 16:14 |
兵庫県 |
| 31 |
虹パパ さん |
2015/10/5 10:19 |
東京都 |
| 32 |
AKIRA さん |
2015/10/5 21:37 |
豊川市 |
| 33 |
スモークマン さん |
2015/10/5 22:31 |
放浪か徘徊か ^^; |
| 34 |
初芝立命館高校 さん |
2015/10/6 9:56 |
|
| 35 |
うさぎとかめ さん |
2015/10/9 20:18 |
|
| 36 |
佐野のくま さん |
2015/10/24 14:14 |
茨城県 |
答えは10cmでした
[
250]
半径を 投稿者:
あめい <10gatu> 投稿日:
2016/10/15(Sat) 17:16
Mr.ダンディさんと同じ求め方をしましたが、半径の5を入力して止まっていました。
[
249]
ところで 投稿者:
dyslexia <10gatu>
投稿日: 2016/10/10(Mon) 22:32
3辺の比が 3: 4: 5 の直角三角形に 内接する円の半径が 1 だということから n個の 等しい円が内接するときの 半径は
5
÷ (2 n + 3 ) と表せます。
[
248]
3,4,5の直角三角形に内接する円の半径は 1 投稿者:
dyslexia <10gatu> 投稿日: 2016/10/05(Wed) 18:25
と云うことは既知の事項として
AB: BC : CA = 3:4:5 の直角三角形には 半径 1 の円が 内接するところから 始めます。
いま 直角三角形 ABCを 内接円の 直径分 すなわち 2だけ ACに 沿って
平行移動させると 同じく直角三角形 abcができ
それにも当然 三辺 3:4:5に対する 半径 1 の円が 内接して 二つの円同士は外接している。
Aと bを延長して交わる点を G
とすると 三角形AGc は 最初の 三角形
ABCと 相似だから 三辺の比も 3:4:5 となるが そこには 二つの円が内接しているから
当然その半径は 縮小されることになる。
今 辺Acは 7になっているから 5に 縮小すると すなわち 5/7倍することになるから 半径も
5/7倍されて 5/7 になる。
そこで問題文に もどると 7 倍されることになるから
結局は 半径 5 になり 直径は 10
[
247]
面積を使わずに・・ 投稿者:
Mr.ダンディ
<10gatu> 投稿日: 2016/10/05(Wed) 11:14
円PとAB,BCとの接点をそれぞれD,E
円QとBC,ACとの接点をそれぞれF,G
Pを通るABの平行線と Qを通るBCの平行線との交点をR
とすると
△PRQ∽△ABC、PQ=2rとなり
PR=2r*(3/5)=(6/5)r
RQ=2r*(4/5)=(8/5)r
AC=AE+EG+GC=AD+2r+FC=(21-11r/5)+2r+(28-13r/5)
∴ 35=49-14r/5
r=5
答えは 5*2=10(cm)
[
246]
訂正;面積から求める 投稿者:
まいすた
<10gatu> 投稿日: 2016/10/03(Mon) 00:49
[
245]
たまにはまじめに 投稿者:
次郎長 <10gatu>
投稿日: 2016/10/01(Sat) 12:10
△ABP+△ACQ+△APQ+△BCQ+△BPQ=△ABC
△APQ=底辺2r、高さr、面積r^2
△BPQ=△BPCー△PQC-△BCQ
△BPQ=底辺28、高さ(r+2r*3/5)*1/2
△BCQもr^2
これを解くと294/5*r=28*21*1/2
r=5
直径10㎝
久しぶりにまじめに解きました。
今日は墓参り、庭掃除、今から松方コレクションと飲み会
来週は旭川。充実の日々。引退はもう少し先
[
244]
面積から求める 投稿者:
まいすた <10gatu>
投稿日: 2016/10/01(Sat) 10:16
[
243]
うーんー、2倍角の公式で・・・・ 投稿者:
巷の夢
<10gatu> 投稿日: 2016/10/01(Sat) 08:18
半径をrとし、∠A、∠Bの正弦値に2倍角の公式を使い、
夫々の正弦値1/2と1/3から斜辺の長さが7rとなる故
r=5、即ち直径は10となる。
[
242]
有名問題 投稿者:
teki <10gatu> 投稿日:
2016/10/01(Sat) 00:23
ですが、証明はそう簡単ではありません。
内接する円の半径をr、直角三角形の3辺の長さを、a、b、cとすると、
r=abc/(a+b)*(a+b+c)
が成立します。
よって内接円の半径は、21*28*35/49*84=5cm
問われているのは直径ですから、10cm となります。(10月の問題にふさわしい数値ですね。)

