9
「今月の問題」 第208回 (平成29年1月)
<問題>
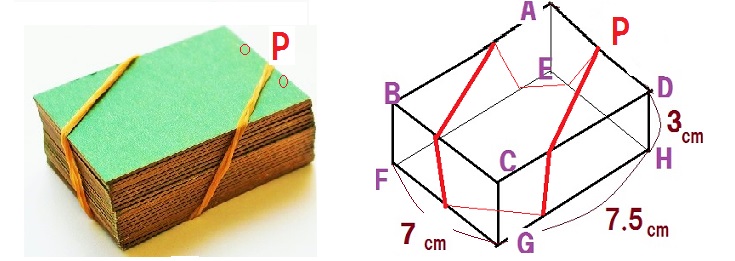
下図を見てください。カードを束ねるために輪ゴムをかけました。
カードを束ねた形は直方体になり、縦7cm、横7.5cm、高さ3cm です。
また、図の点Pは辺ADの中点であり、輪ゴムは必ず点Pを通るものとします。
ここで問題です。輪ゴムが通る経路が最短になるとき、その経路の長さは何cmになるでしょうか。
(※注) 下写真の通り、6つの面を全て通るように、輪ゴムをかけるようにします。
|
 |
<正解者一覧表>
| 順位 |
name |
メール到着日時 |
備 考 |
| 1 |
teki さん |
2017/1/1 0:05 |
大阪府 |
| 2 |
algebra さん |
2017/1/1 0:11 |
神奈川県 |
| 3 |
源内シンガポール さん |
2017/1/1 0:12 |
長崎県 |
| 4 |
男はつらいよ さん |
2017/1/1 0:24 |
神奈川県 |
| 5 |
kou さん |
2017/1/1 0:28 |
さいたま |
| 6 |
バニラ さん |
2017/1/1 0:30 |
|
| 7 |
次郎長 さん |
2017/1/1 0:31 |
兵庫県 |
| 8 |
dyslexia さん |
2017/1/1 3:00 |
大阪府 |
| 9 |
朝霞おじ さん |
2017/1/1 4:43 |
埼玉県 |
| 10 |
巷の夢 さん |
2017/1/1 7:24 |
神奈川県在住 |
| 11 |
まいすた さん |
2017/1/1 9:36 |
|
| 12 |
いちもく さん |
2017/1/1 12:47 |
立川市 |
| 13 |
uchinyan さん |
2017/1/1 13:53 |
|
| 14 |
マッキー27 さん |
2017/1/1 14:57 |
愛知県 |
| 15 |
鯨鯢(Keigei) さん |
2017/1/1 17:14 |
|
| 16 |
Mr.ダンディ さん |
2017/1/2 0:53 |
大阪府 |
| 17 |
ユートニウム さん |
2017/1/2 9:55 |
|
| 18 |
NNR4 さん |
2017/1/2 13:31 |
兵庫県 |
| 19 |
スモークマン さん |
2017/1/2 15:59 |
|
| 20 |
AKIRA さん |
2017/1/2 16:29 |
豊川市 |
| 21 |
GUTENTAG さん |
2017/1/3 10:35 |
滋賀県 |
| 22 |
たかひろ さん |
2017/1/4 20:12 |
埼玉県 |
| 23 |
虹パパ さん |
2017/1/5 16:28 |
東京都 |
| 24 |
りーくん さん |
2017/1/5 23:47 |
埼玉県 |
| 25 |
いぬたこ さん |
2017/1/6 5:02 |
千葉 |
| 27 |
うたねこ さん |
2017/1/6 5:40 |
関東 |
| 28 |
ほかず さん |
2017/1/6 5:41 |
愛知 |
| 29 |
ローリー さん |
2017/1/6 15:40 |
大阪府 |
| 30 |
阿修羅 さん |
2017/1/9 12:38 |
長野県小学校教諭 |
| 31 |
やぶコウノトリ さん |
2017/1/11 10:34 |
兵庫県 |
| 32 |
あめい さん |
2017/1/13 17:38 |
静岡県 |
| 33 |
KAZ さん |
2017/1/14 12:58 |
熊本県 |
| 34 |
市松 さん |
2017/1/19 23:50 |
東京都 |
| 35 |
チェイン さん |
2017/1/25 9:17 |
愛知県 |
| 36 |
あ、そうか さん |
2017/1/28 17:52 |
兵庫県 |
答えは、29 でした
[
288]
あけまして 投稿者:
岡本ボンバーズ <1gatu>
投稿日: 2017/01/17(Tue) 10:35
おめでとうございます。今年もよろしくお願いします。「元号」できましたか。私はよく肉を食べたいときに、この答えになるようにセッティングします。(笑)
[
287]
正月早々忘れて遅くなりました。 投稿者:
ゴンとも
<1gatu> 投稿日: 2017/01/17(Tue) 00:00
今回は7が520.4,7.5が319.8,3が282の問題を見つけ
何も考えずに
sqrt((3+7.5)^2*2^2+(3+7)^2*2^2);29・・・・・・(答え)
これは今年の元号でしたね。
見つけた問題の答えは
sqrt((282+319.8)^2*2^2+(282+520.4)^2*2^2);2006
で出題された西暦でした。
[
286]
累卵の危うき安定 投稿者:
あめい <1gatu>
投稿日: 2017/01/13(Fri) 18:17
あけましておめでとうございます。
書店に行くと、漫画など輪ゴムで一度はずすと元に戻せないような芸術的にとめてある店があります。
半世紀にわたる立ち読み人にはハードルが高いですが、なんかセンスを感じて好きです。
こちらの縛り方も、できてしまえば安定する、しかし再現の難しい縛りで、同じにおいを感じます。
累卵の危うき安定
[
285]
Re:[283] 正解は21cmという説 投稿者:
よしおか
<1gatu> 投稿日: 2017/01/05(Thu) 08:54
>
正月早々、野暮言ってしまいましたが、私なら21cmを正解にします。
おっしゃる通りです。早速、巷の夢さんの助言をもとに、問題文の中に注釈をいれました。
報道関係を見ると、天皇の生前退位の関係で、元号が「平成」を使われるのは、あと暫くの間のみになりそうです。
今回は、平成29年度が始まるにあたり、何とか答えが「29」になることだけを考えて出題させてもらいました。
ただ、写真のとおり6面を輪ゴムで縛りましたが、結構安定はするように思いました。
[
284]
Re:[283] 正解は21cmという説 投稿者:
巷の夢
<1gatu> 投稿日: 2017/01/03(Tue) 13:08
なる程、今回の問題は、図に描かれているように直方体の6面
全てをかけひもが通らねばならないのですね。
これが問題文の中に書かれていない為、デアルケ様の考え方にも
一理ありますが・・・、そこは図の様にひもをかけると理解し、
問題を楽しみましょう・・・。
[
283]
正解は21cmという説 投稿者:
デアルケ
<1gatu> 投稿日: 2017/01/03(Tue) 01:34
正解=21cmというのは如何でしょう? 29㎝より小さいですし、点Pを通っているし、直方体を形成します。 設問の条件を間違いなくすべてクリアしています。
通称一文字掛けと言われる掛け方ですね。
また、29㎝を正解とする掛け方は安定せず机上の空論解です
正月早々、野暮言ってしまいましたが、私なら21cmを正解にします。
[
282]
あけましておめでとうございます 投稿者:
スモークマン <1gatu> 投稿日:
2017/01/02(Mon) 15:00
展開図で解けばいいとは思ったものの…
計算せず,初問はキットと,いくつかで認証(一番効率のいい方法^^)しちゃいましたわ Orz~☆
やっぱりでグラッチェ♪
今年もよろしくお願いいたします~m(_ _)m~v
[
281]
明けましておめでとうございます 投稿者:
Mr.ダンディ
<1gatu> 投稿日: 2017/01/02(Mon) 01:01
ビリヤードでの問題はよくあるのですが、箱にかけるひもを使った問題は初めてでした。
面白い問題で楽しめました。
(今月も1日遅れの参加になってしまいました)
本年もよろしくお願いいたします。
[
280]
難しかった 投稿者:
次郎長 <1gatu> 投稿日:
2017/01/01(Sun) 22:45
明けましておめでとうございます。
親族郎党集まって、夕方5時から今まで飲んで食っておしゃべりしてました。
こういう問題は、展開図を描いて直線になる、ということは知識として知っていましたが、
今回はイメージできず。A4用紙で箱を作って、答えを求めました。
20^2+21^2が29^2になることは、今回初めて知りました。
難しかったです。
[
278]
展開図上で直線ですね 投稿者:
まいすた <1gatu>
投稿日: 2017/01/01(Sun) 09:34
[
277]
ちょっと戸惑いました・・・ 投稿者:
巷の夢
<1gatu> 投稿日: 2017/01/01(Sun) 07:31
吉岡先生、明けましておめでとうございます。本年も興味深い
問題の御教授方宜しくお願い申し上げます。
今回の問題は直角三角形の2辺が20と21になり平方根が開けない
のではと思いながら計算すると・・・、あら不思議綺麗な値に
なるのですね。勉強になりました。

