「今月の問題」 第209回 (平成29年2月)
<問題>
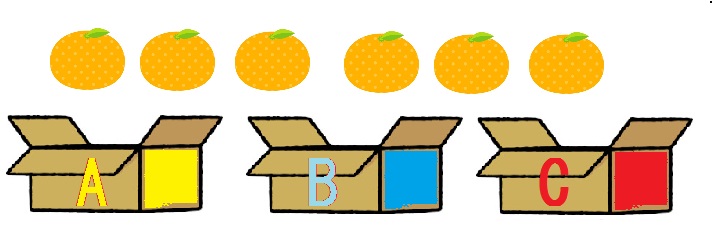
下図を見てください。ミカンが6個あります。この6個のミカンを全てA、B、Cのどれかのミカン箱に入れようと思います。
ここで問題です。入れ方は何通りあるでしょうか。
ただし、空の箱があってもかまいません。たとえば、(A,B,C)=(6,0,0)、(4,2,0)でもOKです。
|
 |
<正解者一覧表>
| 順位 |
name |
メール到着日時 |
備 考 |
| 1 |
kou さん |
2017/2/1 0:04 |
さいたま |
| 2 |
ゴンとも さん |
2017/2/1 0:05 |
豊川市 |
| 3 |
algebra さん |
2017/2/1 0:06 |
神奈川県 |
| 4 |
源内シンガポール さん |
2017/2/1 0:07 |
長崎県 |
| 5 |
男はつらいよ さん |
2017/2/1 0:07 |
神奈川県 |
| 6 |
朝霞おじ さん |
2017/2/1 0:08 |
埼玉県 |
| 7 |
バニラ さん |
2017/2/1 0:09 |
|
| 8 |
Mr.ダンディ さん |
2017/2/1 0:12 |
大阪府 |
| 9 |
デアルケ さん |
2017/2/1 0:15 |
三重県紀北町 |
| 10 |
teki さん |
2017/2/1 0:23 |
大阪府 |
| 11 |
いちもく さん |
2017/2/1 4:28 |
立川市 |
| 12 |
鯨鯢(Keigei) さん |
2017/2/1 5:20 |
|
| 13 |
マッキー27 さん |
2017/2/1 5:28 |
愛知県 |
| 14 |
巷の夢 さん |
2017/2/1 5:44 |
神奈川県在住 |
| 15 |
次郎長 さん |
2017/2/1 6:54 |
|
| 16 |
寒いです さん |
2017/2/1 7:11 |
兵庫県 |
| 17 |
虹パパ さん |
2017/2/1 9:02 |
東京都 |
| 18 |
uchinyan さん |
2017/2/1 9:43 |
|
| 19 |
AKIRA さん |
2017/2/1 11:00 |
豊川市 |
| 20 |
NNR4 さん |
2017/2/1 19:21 |
兵庫県 |
| 21 |
ユートニウム さん |
2017/2/1 21:17 |
|
| 22 |
dyslexia さん |
2017/2/1 22:34 |
大阪府 |
| 23 |
まいすた さん |
2017/2/1 23:15 |
|
| 24 |
★I am GOD★ さん |
2017/2/1 23:30 |
ださいたま |
| 25 |
GUTENTAG さん |
2017/2/2 13:39 |
滋賀県 |
| 26 |
チェイン さん |
2017/2/2 17:09 |
愛媛県 |
| 27 |
阿修羅 さん |
2017/2/2 21:04 |
長野県小学校教諭 |
| 28 |
スモークマン さん |
2017/2/4 23:05 |
@新倉敷 |
| 29 |
たかひろ さん |
2017/2/6 8:58 |
埼玉県 |
| 30 |
┌(┌^o^)┐ さん |
2017/2/7 22:25 |
和歌山県 |
| 31 |
岡本ボンバーズ さん |
2017/2/8 10:58 |
秋田県 |
| 32 |
初芝立命館高等学校 さん |
2017/2/8 17:11 |
大阪府 |
| 33 |
KAZ さん |
2017/2/9 19:04 |
熊本県 |
| 34 |
りーくん さん |
2017/2/9 23:13 |
埼玉県 |
| 35 |
あめい さん |
2017/2/10 13:05 |
静岡県 |
| 36 |
うさぎとかめ さん |
2017/2/12 10:44 |
|
| 37 |
かず さん |
2017/2/13 9:18 |
大阪 |
| 38 |
DSK さん |
2017/2/15 10:49 |
|
答えは、28 でした
[
303]
学んだか、学ばないか。 投稿者:
あめい <3gatu>
投稿日: 2017/02/10(Fri) 13:18
私の県では(全国的?)重複組み合わせは、現在60歳以上の方(何歳までかわかりませんが)は高校のカリキュラムの中に入っていましたが、59歳から(何年間かは?)削除されていました。複素平面などもなかったです。かわりにベクトルが入ったような気がします。
そのせいか、(次郎長さんと同様?)何度も覚えようと見て、その場は何となく覚えたようになるのですが、すぐ忘れます、私の場合”そのせい”でもないのでしょうが・・・。
[
302]
Re:[301] 重複組合せ 投稿者:
巷の夢
<3gatu> 投稿日: 2017/02/03(Fri) 06:41
> 重複組合せが議論になっていますので一言。
>
箱に入れる蜜柑が0個でもいいなら、6個の蜜柑の間だけでなく、両端に区切りを入れてもよく、
> また、同じ場所に2個の区切りを入れてもいいので 7H2=28
になります。
> 7H2=8C2
ですが、これは、箱の数だけ蜜柑を増やし、
>
9個の蜜柑をどの箱にも1個以上入れる方法が 8C2 通りで、
>
それぞれの箱から1個ずつ蜜柑を取り去ると、問題の条件に合致しますので、7H2 と表されます。
> このように考えれば、nHr=(n+r-1)Cr が得られます。
7H2=28 なる程そうですね、鯨鯢(Keigei) 様の非常に分かり易い説明で今までもやもやしていた
重複組み合わせの考え方が、はっきり致しました。有難うございました
[
301]
重複組合せ 投稿者:
鯨鯢(Keigei)
<3gatu> 投稿日: 2017/02/01(Wed) 18:56
重複組合せが議論になっていますので一言。
6個の蜜柑の間5ヶ所から2ヶ所を選んで区切りを入れ、
左の区切りの左の蜜柑を箱A,2つの区切りの間の蜜柑を箱B,右の区切りの右の蜜柑を箱Cに入れることにすれば、
3つの箱に1個以上の蜜柑が入ることになり、その方法は 5C3=10 通りです。
箱に入れる蜜柑が0個でもいいなら、6個の蜜柑の間だけでなく、両端に区切りを入れてもよく、
また、同じ場所に2個の区切りを入れてもいいので
7H2=28 になります。
7H2=8C2 ですが、これは、箱の数だけ蜜柑を増やし、
9個の蜜柑をどの箱にも1個以上入れる方法が
8C2 通りで、
それぞれの箱から1個ずつ蜜柑を取り去ると、問題の条件に合致しますので、7H2 と表されます。
このように考えれば、nHr=(n+r-1)Cr が得られます。
>
ところで、私が高校生であった40年前には、重複の組み合わせ問題は、教科書になかったように思うのですが、私がさぼっていたのでしょうか。
とありますが、私自身は覚えておりません。
ただ、順列・重複順列・組合せを知り、それなら重複組合せもあるだろうと思って調べました。
教科書にあるかないかに関係なく、便利なら使おうというのが私のスタンスです。
なお、管理人さんの 3H6
もよく使われる解き方で、このように書いてある参考書も多いと思いますが、
空の箱を認める・認めないに関わらず同じ様に区切りで解ける上記の方法が私は気に入っています。
[
300]
Re:[298] そうか 投稿者:
Mr.ダンディ
<3gatu> 投稿日: 2017/02/01(Wed) 13:14
> 全く同意。そうですよね。私が高校生だった頃は50年前ですが、
> その時も重複組み合わせはなかったような。
私が高校生だったのは 56~53年前ですが
「重複組み合わせはなかった」どころか、「確率」という単元自体がなかったように思います。
理系のクラスにいたので 選択をしなかったというのでもなく、大学受験に向けて確率の勉強
をした記憶もないですね。
(その後「確率」がどんどん入ってきたようには思いますが・・)
[
299]
Re:[297]&[298] そうか 投稿者:
巷の夢
<3gatu> 投稿日: 2017/02/01(Wed) 11:02
> ところで、私が高校生であった40年前には、重複の組み合わせ問題は、
教科書になかったように思うのですが、
私がさぼっていたのでしょうか。
昔は高校では教えていなかったとのご指摘大いに興味があります。
しかし、今回の様な問題は昔からあったのですから、どの様な
解法を教えていたのでしょうか・・・・?
Mr.ダンディ 様の解法の様に先生が教えていたのでしょうか?
[
298]
Re:[297] そうか 投稿者:
次郎長
<3gatu> 投稿日: 2017/02/01(Wed) 10:51
>
ところで、私が高校生であった40年前には、重複の組み合わせ問題は、教科書になかったように思うのですが、私がさぼっていたのでしょうか。
全く同意。そうですよね。私が高校生だった頃は50年前ですが、
その時も重複組み合わせはなかったような。それで未だに重複組み合わせになったとたんに
分からなくなるのです。数学の授業は好きだったのでサボった記憶はないのですが。
[
297]
Re:[292] そうか 投稿者:
管理人
<3gatu> 投稿日: 2017/02/01(Wed) 08:22
> 今回の問題は208回でしたね。
> それで28が答えとなるように設定されたのですよね。
皆さんの訪問いつもありがとうございます。
日常的な生活の中に算数・数学問題がないかと考えるのですが・・・・・。
今回は2月ということで、答が28(3H6)になるようにしました。
ところで、私が高校生であった40年前には、重複の組み合わせ問題は、教科書になかったように思うのですが、私がさぼっていたのでしょうか。
[
296]
私は重複組み合わせが分からない 投稿者:
次郎長
<3gatu> 投稿日: 2017/02/01(Wed) 08:06
私は昔から、重複組み合わせが分からない。
覚えてしあめば良いと思いながら、それができない。
いつも、nHrのどちらがrか分からない。
今回はAの箱に6個入れたときは残りは0個、その2個をB,Cに入れる組み合わせは1
Aに5個なら、残りは1個、組み合わせは2
Aに4個なら、残りは2個、組み合わせは3
Aに3個なら、残りは3個、組み合わせは4
Aに2個なら、残りは4個、組み合わせは5
Aに1個なら、残りは5個、組み合わせは6
Aに0個なら、残りは6個、組み合わせは7
合計28組み合わせ
4箱だったら困りました。
[
295]
重複組み合わせの幸せ・・・・? 投稿者:
巷の夢
<3gatu> 投稿日: 2017/02/01(Wed) 05:52
鯨鯢(Keigei) 様と同じく、重複組み合わせで
解きました。いつも感心するのですが、この組
合わせの考え方は秀逸ですね。
Mr.ダンディ 様の普通の組み合わせの考え方も
味があって素晴らしいですね。
[
294]
208回 投稿者:
鯨鯢(Keigei) <3gatu>
投稿日: 2017/02/01(Wed) 05:23
重複組合せ 7H2=28 で一発。
[
293]
あかん、ボケてる。 投稿者:
teki <3gatu>
投稿日: 2017/02/01(Wed) 00:38
209回でしたね。
失礼しました(^^;;
[
292]
そうか 投稿者:
teki <3gatu> 投稿日:
2017/02/01(Wed) 00:34
今回の問題は208回でしたね。
それで28が答えとなるように設定されたのですよね。
[
291]
箱を区別するのか、しないのか 投稿者:
teki
<3gatu> 投稿日: 2017/02/01(Wed) 00:26
で少し悩みましたが、問題図でA,B,Cとしているのと、色分けしているので、区別するものとして解きました。
解き方は、Mr.ダンディ
さんと全く同じで、8C2=28 通り となりました。
[
290]
簡単でした。 投稿者:
Mr.ダンディ <3gatu>
投稿日: 2017/02/01(Wed) 00:14
6つの○と 2本の仕切り|の並べ替え方の数
8C2=28(通り)
[
289]
十進Basic で 投稿者:
ゴンとも <3gatu>
投稿日: 2017/02/01(Wed) 00:07
FOR a=0 TO 6
FOR b=0 TO 6
FOR c=0 TO 6
IF a+b+c=6 THEN LET
s=s+1
NEXT c
NEXT b
NEXT a
PRINT s
END
f9押して 28・・・・・・(答え)

