「今月の問題」　第２１１回　（平成２９年４月）
 
＜問題＞　

　

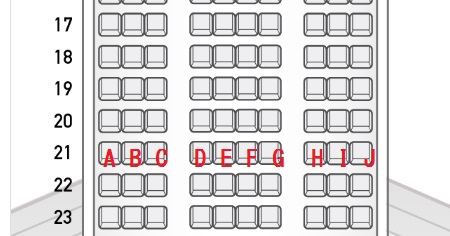
右図はＨＰで確認したANAボーイング777の座席図です。
よしお君の家族３人を含めた１０人がくじを引いて、A B C 通路 DEFG通路HIJの１０席の座席を予約したいと考えます。

ここで問題です。よしお君の家族3人の誰もが、隣同士にならない確率を分数で答えて下さい。


ただし、通路を挟んだ席は隣同士の席ではないものと考えて下さい。

 

 

＜正解者一覧表＞　 　　　　　　
順位 　　　　ｎａｍｅ　　　 　　メール到着日時 　　 　　備　考　　
　１ algebra　さん 2017/4/1　0:33 神奈川県　
　２ 男はつらいよ　さん 2017/4/1　0:39 神奈川県　
　３ Mr.ダンディ　さん 2017/4/1　0:40 大阪府　
　４ ＧＯＧＯＧＩＡＮＴＳ　さん 2017/4/1　0:47 　
　５ Bトレマン　さん 2017/4/1　0:50 鉄道大好き　
　６ kou　さん 2017/4/1　1:26 　
　７ バニラ　さん 2017/4/1　3:53 　
　８ 巷の夢　さん 2017/4/1　6:02 神奈川県在住　
　９ いぬたこ　さん 2017/4/1　6:03 千葉県　
１０ 鯨鯢(Keigei)　さん 2017/4/1　6:41 　
１１ うたねこ　さん 2017/4/1　6:49 東京・　
１２ ほかず　さん 2017/4/1　6:51 愛知　
１３ リリー山本　さん 2017/4/1　6:52 愛知県　
１４ 次郎長　さん 2017/4/1　7:46 桜固し、兵庫県
１５ いちもく　さん 2017/4/1　8:51 立川市　
１６ uchinyan　さん 2017/4/1　13:29 　
１７ スモークマン　さん 2017/4/1　19:45 ＠新倉敷　
１８ 角散のど飴　さん 2017/4/1　21:19 立川市　
１９ NNR4　さん 2017/4/1　23:32 兵庫県　
２０ ユートニウム　さん 2017/4/3　11:17 　
２１ まいすた　さん 2017/4/3　23:34 　
２２ やぶコウノトリ　さん 2017/4/4　11:27 兵庫県　
２３ ゴンとも　さん 2017/4/4　19:46 豊川市　
２４ たかひろ　さん 2017/4/5　9:36 埼玉県　
２５ 市松　さん 2017/4/14　19:27 東京都　

答えは　17/30　でした

[319] 無題 投稿者： 市松 <5gatu> 投稿日： 2017/04/14(Fri) 22:02  
隣同士にならない場合を数えて求めました。
もっとスマートにやりたかったのですが。
[318] 十進Basic で 投稿者： ゴンとも <5gatu> 投稿日： 2017/04/04(Tue) 20:02  
十進Basic で

よしお君の家族を1,2,3として残りを4,5,6,7,8,9,10として

print time$
FOR a=1 to 10
FOR b=1 to 10
if b=a or (a=1 and b=2) or (a=2 and b=1) or (a=1 and b=3) or (a=3 and b=1) or (a=2 and b=3) or (a=3 and b=2) then goto 80
FOR c=1 to 10
if c=a or c=b or (b=1 and c=2) or (b=2 and c=1) or (b=1 and c=3) or (b=3 and c=1) or (b=2 and c=3) or (b=3 and c=2) then goto 70
FOR d=1 to 10
if d=a or d=b or d=c then goto 60
FOR e=1 to 10
if e=a or e=b or e=c or e=d or (d=1 and e=2) or (d=2 and e=1) or (d=1 and e=3) or (d=3 and e=1) or (d=2 and e=3) or (d=3 and e=2) then goto 50
FOR f=1 to 10
if f=a or f=b or f=c or f=d or f=e or (e=1 and f=2) or (e=2 and f=1) or (e=1 and f=3) or (e=3 and f=1) or (e=2 and f=3) or (e=3 and f=2) then goto 40
FOR g=1 to 10
if g=a or g=b or g=c or g=d or g=e or g=f or (f=1 and g=2) or (f=2 and g=1) or (f=1 and g=3) or (f=3 and g=1) or (f=2 and g=3) or (f=3 and g=2) then goto 30
FOR h=1 to 10
if h=a or h=b or h=c or h=d or h=e or h=f or h=g then goto 20
FOR i=1 to 10
if i=a or i=b or i=c or i=d or i=e or i=f or i=g or i=h or (h=1 and i=2) or (h=2 and i=1) or (h=1 and i=3) or (h=3 and i=1) or (h=2 and i=3) or (h=3 and i=2) then goto 10
FOR j=1 to 10
if j=a or j=b or j=c or j=d or j=e or j=f or j=g or j=h or j=i or (i=1 and j=2) or (i=2 and j=1) or (i=1 and j=3) or (i=3 and j=1) or (i=2 and j=3) or (i=3 and j=2) then goto 5
let s=s+1
5 next j
10 next i
20 next h
30 next g
40 next f
50 next e
60 next d
70 next c
80 next b
90 next a
print s/3628800
print time$
END

有理数モードにしてf9押して

19:29:17
17/30・・・・・・(答え)
19:30:18

今回はリアルタイムどころか数日遅れでやってないことに
気付きました。先月は翌朝に気付いたみたいです。問題自体は今回もすぐ解けたのですが・・・
またここ数カ月,答えの数値も送ってないことが発覚しました。
今さっき送りました。(有理数モードにしてがないから書き直しで・・・)これからもよろしくお願いします。
[317] スマートに行けない 投稿者： まいすた <5gatu> 投稿日： 2017/04/03(Mon) 23:33  
10席に3人を配置すると10C3=120通り。

それぞれの2人目の座る位置に対して、隣り合わない場合は、

2人目の位置
↓
B：（必ずAにいる1人目と隣り合うので）0通り
C：（1人目はA、3人目はE～J）1×7通り
D：（1人目はA～C、3人目はF～J）3×5通り
E：（1人目はA～C、3人目はG～J）3×4通り
以下対称で、
合計68通り。

答え：68/120=17/30

http://primzahl.seesaa.net/

[316] 入れたぁ^^ 投稿者： スモークマン <5gatu> 投稿日： 2017/04/01(Sat) 19:47  
*1*1*1*・・・真ん中の*は必ず１個あり、
so…4H(10-5)=8C3=56
**1/1***/***　・・・あと1ヶ所は入れるところは…6ヶ所
so…2*6=12
so…(56+12)/10C3=68/120=18/30
で…♪

それにしても最近眠くて眠くて…
次郎長さんはいつもお元気で羨まし☆
[315] 混乱してしまった 投稿者： 次郎長 <5gatu> 投稿日： 2017/04/01(Sat) 09:40  
>通路を挟んだ席は隣同士の席ではない
というところがどうもうまく理解できずに、
ＣＤＦ、ＣＤＧ、ＣＤＨ、ＣＤＩ，ＣＤＪの5通りが頭に残らず、何度も誤答しました。
すぐに解けると思ったので、薄着でパソコンに向かい、体が冷えてしまいました。
さぁ、4月ですね。月曜は入社式です。
[314] Re:[312] 地道に計算・・・・ 投稿者： 巷の夢 <5gatu> 投稿日： 2017/04/01(Sat) 08:15  
申し訳ございません。
> １０席に３人が座るのは１０H３=７２０通り、
　は１０P３=７２０通りの間違いでした。
[313] 座席がもっと多くても 投稿者： 鯨鯢(Keigei) <5gatu> 投稿日： 2017/04/01(Sat) 07:22  
座席がもっと多くても次のように計算できます。

座席を 1，2，3，5，6，7，8，10，11，12 とし、通路を 4，9 とします。
2～11 の中から３個の数を選び方は 10Ｃ3＝120通り、
最小数から１を減じ、最大数に１を加えて３つの席を選べば隣り合いません。
そのうち、通路4を選ぶのは、4より小さい数(1，2)と 4より大きい数(6～12)を選ぶ 2･7＝14通りと、
4より大きい数２個を 6～11 から選び大きいほうに１を加える 6Ｃ2＝15通りの 計29通り、
通路9を選ぶのも同様に、29通り、
通路4，9の両方を選ぶのは もう１つが 1，2，6，7，11，12 の 6通り、
通路が含まれるのは全部で、29＋29－6＝52 通り、
よって、隣り合わない３つの席は 120－52＝68 通りです。
３つの席の選び方は 10Ｃ3＝120通りですので、確率は 68/120＝17/30 です。
[312] 地道に計算・・・・ 投稿者： 巷の夢 <5gatu> 投稿日： 2017/04/01(Sat) 06:27  
１０席に３人が座るのは１０H３=７２０通り、A～Cに２人、D～Gに２人、
H～Jに２人とし、その他の７席、７席および６席に１人座るのが
４２通り、４２通りおよび１０８通り、そしてA～C、D～Gおよび
～Jに１人づつの場合が２１６通り、即ち、４０８/７２０＝１７/３０
[311] 無題 投稿者： いぬたこ <5gatu> 投稿日： 2017/04/01(Sat) 06:00  
三列ならび4通り 二列ならび7×7-1 計52通り 10c3 120。 120-52 68
答は68/120