「今月の問題」　第２１２回　（平成２９年５月）
＜問題＞　
　下図１のように、２×２のマス目に、正の整数１と２と３と５をあてはめます。
　下 図２のような形の部分（回転させたものを含みます）について、そこに含まれる整数の和をとると、どのような数になるか考えました。
 １と２と３と５の場合、下図３のように、１１までの正の整数全てが出来ます。

 ここで問題です。
　 １からある整数までの全ての正の整数ができるように、入れる４つの数字を工夫すれば、最大いくつまでの整数を作ることが出来るでしょうか。

※問題の意味が分かりにくかったようです。鯨鯢さんに修正していただきました。

 

正解者一覧表＞　 　　　　　　　　　　　　　　　　
順位 　　　　ｎａｍｅ　　　 　　メール到着日時 　　 　　備　考　　
　１ kou　さん 2017/5/1　0:08 さいたま　
　２ デアルケ　さん 2017/5/1　0:11 三重県紀北町　
　３ スモークマン　さん 2017/5/1　0:13 ＠新倉敷　
　４ ゴンとも　さん 2017/5/1　0:19 豊川市　
　５ 次郎長　さん 2017/5/1　0:20 眠れぬ兵庫県　
　６ Mr.ダンディ　さん 2017/5/1　1:01 大阪府　
　７ algebra　さん 2017/5/1　1:12 神奈川県　
　８ 男はつらいよ　さん 2017/5/1　1:16 神奈川県　
　９ NNR4　さん 2017/5/1　1:29 兵庫県　
１０ いぬたこ　さん 2017/5/1　3:56 千葉　
１１ うたねこ　さん 2017/5/1　4:15 関東　
１２ ほかず　さん 2017/5/1　4:16 愛知　
１３ 山本フランキー　さん 2017/5/1　4:17 愛知県　
１４ 巷の夢　さん 2017/5/1　5:44 神奈川県在住　
１５ 鯨鯢(Keigei)　さん 2017/5/1　5:51 　
１６ いちもく　さん 2017/5/1　6:39 立川市　
１７ uchinyan　さん 2017/5/1　8:36 　
１８ バニラ　さん 2017/5/1　9:37 　
１９ 朝霞おじさん　さん 2017/5/1　14:21 埼玉県　
２０ ＧＯＧＯＧＩＡＮＴＳ　さん 2017/5/1　14:58 　
２１ ユートニウム　さん 2017/5/1　15:04 　
２２ teki　さん 2017/5/1　20:44 大阪府　
２３ まいすた　さん 2017/5/1　22:02 　
２４ dyslexia　さん 2017/5/1　22:59 大阪府　
２５ マッキー２７　さん 2017/5/2　17:35 愛知県　
２６ 阿修羅　さん 2017/5/2　20:40 長野県小学校教諭　
２７ 市松　さん 2017/5/3　1:09 東京都　
２８ りーくん　さん 2017/5/3　20:44 埼玉県　
２９ そんなの関係ねえ　さん 2017/5/3　21:50 　
３０ KAZ　さん 2017/5/4　11:53 熊本県　
３１ 行事　さん 2017/5/5　9:18 　
３２ たかひろ　さん 2017/5/7　15:18 埼玉県　
３３ 石原塾　さん 2017/5/30　15:39 　
３４ カメカメ　さん 2017/5/30　18:02 広島県　

 

こたえは、１３でした。

[329] 無題 投稿者： 市松 <6gatu> 投稿日： 2017/05/03(Wed) 01:05  
斜めがダメというところで少し引っかかりました。
しかし、スッキリしないなぁ、と思っていたのですが、鯨鯢(Keigei)様の考え方で、なるほど、となりました。
[328] Re:[327] 問題文が？ 投稿者： 巷の夢 <6gatu> 投稿日： 2017/05/02(Tue) 08:58  
鯨鯢(Keigei)様の
「図２のような形の部分(回転させたものを含みます)」は
13通りしかないので、最大でも 13で・・・・・・

　で納得した次第です。
[327] 問題文が？ 投稿者： 鯨鯢(Keigei) <6gatu> 投稿日： 2017/05/01(Mon) 22:41  
最初、「入れる４つの数字を工夫すれば、１１よりも大きい全ての正の整数ができるようです。」
の意味が理解できませんでした。
「１１よりも大きい全ての正の整数ができる」を、「１から１１まではできてもできなくても良い」
と解釈し、12，1，2，16 と入れれは、12 から 19 までできますが、そうではなかったようです。
「１からある整数までの全ての正の整数ができるように、入れる４つの数字を工夫すれば、
最大いくつまでの整数を作ることが出来るでしょうか。」とすれば、誤解はないと思います。
なお、図３の図には「図２」と書かれています。

出題者の意図が理解できれば、あとは簡単、「図２のような形の部分(回転させたものを含みます)」は
13通りしかないので、最大でも 13で、1，2，4，6 や 1，3，7，2 と入れれは、1 から 13 までできます。
[326] 無題 投稿者： まいすた <6gatu> 投稿日： 2017/05/01(Mon) 22:00  
類題として、5マスまたは6マスを環状に配置しても同じことができますね。

http://primzahl.seesaa.net/

[325] 問題文が 難解？ 投稿者： dyslexia <6gatu> 投稿日： 2017/05/01(Mon) 18:06  
完全数 6 が すぐに頭に浮かんだので 1,2,3, の三数で

2
3 1 と並べれば 6 まで作れるので 残りひとつは

7 以上 で 先ずは 右上に 7 をいれると 13まで作れる
しかし 7より大きい正数をいれると 6と その数のあいだの正数が
作れないので 7が限界値では ないでしょうか
そんなんで 答えは 13 でしょうか

[324] 無題 投稿者： 無名 <6gatu> 投稿日： 2017/05/01(Mon) 14:12  
4数字だけなら1,2,4,7で14となるんだが、2X2マスというのが
ミソでしたね。いい問題ですね。
[323] 拙者ひよこでござる 投稿者： ひげぴよ <6gatu> 投稿日： 2017/05/01(Mon) 08:47  
最初、１４かと思ったが、ななめは足せないことに気づき、
やり直しとなった。意外と理詰めでやると難問である。
[322] 試行錯誤で・・・・ 投稿者： 巷の夢 <6gatu> 投稿日： 2017/05/01(Mon) 06:57  
問題文から、最大数は１２か１３であろうと推定し、１２と
すると１、２、３及び６ではどの様に組み合わせても二つの
数が出来ない。
では、１、２、４及び６なら良いだろうと試すと、全てOKと
なり、めでたしめでたし・・・。
何ともひどい説明ですが、簡潔な解き方は・・・？これから
皆様の回答で勉強致します。
[321] うーん 投稿者： いぬたこ <6gatu> 投稿日： 2017/05/01(Mon) 03:53  
ななめだめ
[320] 真夜中で疲れました。 投稿者： ゴンとも <6gatu> 投稿日： 2017/05/01(Mon) 03:14  
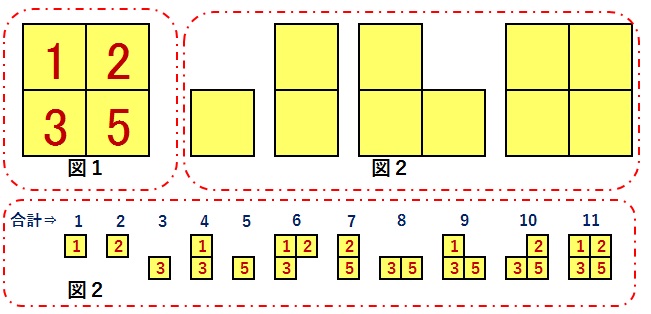
足し算ばかりで最大を求めるのだから1,2の二つはありこれで1,2,3はでき
{1,2,3},{1,2,4}・・・・・・(考察する3個の数の組み)
1,2,5として4が飛んで不可なのでこれ以降5のところが6以降ですべて不適

{1,2,4}であと1つaとすると斜めが違う置き方は
1を固定して回転して同じものを除き以下の2通り

(a)
1,4
a,2
(a-1):1,2,4,a
(a-2):a+1,a+2,5,6
(a-3):a+3,a+5,a+6,7
(a-4):a+7
(total):a,a+1,a+2,a+3,a+5,a+6,a+7,1,2,4,5,6,7
ここで3がとれないから
a=3で(total):3,4,5,6,8,9,10,1,2,4,5,6,7:10まで・・・・・・(1)

(b)
1,2
a,4
(b-1):1,2,4,a
(b-2):a+1,a+4,3,6
(b-3):a+3,a+5,a+6,7
(b-4):a+8
(total):a,a+1,a+3,a+4,a+5,a+6,a+7,1,2,3,4,6,7
ここで5がとれないから
a=5で(total):5,6,8,9,10,11,12,1,2,3,4,6,7:12まで・・・・・・(2)

{1,2,3}であと1つaとすると斜めが違う置き方は
1を固定して回転して同じものを除き以下の2通り

(c)
1,3
a,2
(c-1):1,2,3,a
(c-2):a+1,a+2,4,5
(c-3):a+3,a+4,a+5,6
(c-4):a+6
(total):a,a+1,a+2,a+3,a+4,a+5,a+6,1,2,3,4,5,6
7以降とれないから
a=7で(total):7,8,9,10,11,12,13,1,2,3,4,5,6:13まで・・・・・・(3)
ここで問題文の例は
a=5で(total):5,6,7,8,9,10,11,1,2,3,4,5,6:11まで・・・・・・(4)
a=6で(total):6,7,8,9,10,11,12,1,2,3,4,5,6:12まで・・・・・・(5)

(d)
1,2
a,3
(d-1):1,2,3,a
(d-2):a+1,a+3,3,5
(d-3):a+3,a+4,a+5,6
(d-4):a+6
(total):a,a+1,a+3,a+4,a+5,a+6,1,2,3,5,6
4がとれないから
a=4で(total):4,5,7,8,9,10,1,2,3,5,6:10まで・・・・・・(6)

以上より最大は(3)で
1,3
7,2　において13・・・・・・(答え)