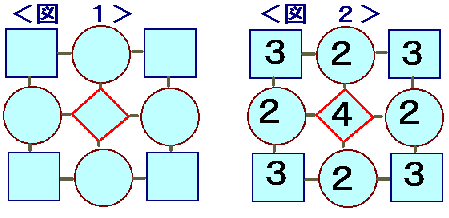
ただし、○と□と◇は別の数字であり、同じ枠の中には同じ数字を入れることにします。
例えば、<図2>のように数字をあてはめると、縦・横に並んだ3つの和は8になります。
数の入れ方は何通りあるでしょうか。

|
|
<図1>で、○と□と◇に1けたの自然数を入れて、縦・横に並んだ3つの和が全て等しくなるようにしたいと考えます。 ただし、○と□と◇は別の数字であり、同じ枠の中には同じ数字を入れることにします。 例えば、<図2>のように数字をあてはめると、縦・横に並んだ3つの和は8になります。 数の入れ方は何通りあるでしょうか。 |
<解答例>
******浜田さん の解答***************
今回はKSP(KSDではありません)で作ってみました。毎回違うソフトでプ
ログラムを作ってみようと考えています。
このプログラムにより,答は32通りになります。
<KSP>
<TIT> "平成12年12月 今月の問題"
<WIN> "640"480"0"0"
<CLS> "0"
<IRO> "0"0"0"
<FONT> "0"18"0"
<POS> "180"110"
<BUT> "P001"
<POS> "260"110"
<DISP> "計算開始"
<STOP>
;
P001
<MOVE> "*kotae"0"
<MOVE> "*A"0"
;
P002
<+> "*A"1"
<MOVE> "*B"0"
;
P003
<+> "*B"1"
<IF> "*A"="*B"
<GOTO> "P004"
<MOVE> "*wa"*A"
<+> "*wa"*A"
<+> "*wa"*B"
<MOVE> "*C"*wa"
<-> "*C"*B"
<-> "*C"*B"
<IF> "*C"="*A"
<GOTO> "P004"
<IF> "*C"="*B"
<GOTO> "P004"
<IF> "*C"<"1"
<GOTO> "P004"
<IF> "*C"<="9"
<+> "*kotae"1"
;
P004
<IF> "*B"<"9"
<GOTO> "P003"
;
P005
<IF> "*A"<"9"
<GOTO> "P002"
;
<DISP> "*kotae"
<STOP>
********
高橋さん の解答************
○+□+□=○+◇+○から、□+□=◇+○ つまり、◇と○がともに偶数ま
たは奇数の時に(◇と○の間に)□がひとつ存在することになります。
ともに奇数のとき、1,3,5,7,9から◇は5通り、○は4通りで20通り。
ともに偶数の時、2,4,6,8から◇は4通り、○は3通りで12通り。
合計で32通りになります。
***** 畠山さん の解答ここから***********
□に入る数をx、○に入る数をy、◇に入る数をzとする。
まずx,y,zの重複を考慮せずに考える。
条件より
2x+y=2y+z
すなわち
z=2x-y (1)
またx,y,zは1桁の自然数であるから
0<x<10 (2)
0<y<10 (3)
0<z<10 (4)
(1),(4)より
0<2x-y<10
すなわち
y<2x かつ 2x-10<y (5)
(2),(3),(5)を満たすのは、図のグレーの部分(境界は除く)内のx,y自然数の格子点である。
0<x<5では
x=1のときy=1で1組
xが1大きくなるごとに、条件を満たす格子点の数は2増えるから
x=2で3組
x=3で5組
x=4で7組
したがってx<5では1+3+5+7=16通りある。
また5<x<10も0<x<5と同じ数だけある。
x=5では=9通りある。
よって組み合わせは16×2+9=41通りである。
次に重複している組み合わせを考える。
(a)x=yの場合 図のy=x上の格子点の9通りである。
(b)y=zの場合 (1)よりy=2x-y、すなわちx=yで(a)の場合に含まれる。
(c)x=zの場合 (1)よりx=2x-y、すなわちx=yで(a)の場合に含まれる。
したがって重複している点はx=y(=z)である9通りである。
以上より求める組み合わせは41-9=32通りである。
******圭太さん の解答*********
(□,○,◇)とすれば、
(2,1,3),(3,1,5),(4,1,7),(5,1,9),(3,2,4),(4,2,6),(5,2,8),
(2,3,1),(4,3,5),(5,3,7),(6,3,9),(3,4,2),(5,4,6),(6,4,8),
(3,5,1),(4,5,3),(6,5,7),(7,5,9),(4,6,2),(5,6,4),(7,6,8),
(4,7,1),(5,7,3),(6,7,5),(8,7,9),(5,8,2),(6,8,4),(7,8,6),
(5,9,1),(6,9,3),(7,9,5),(8,9,7)
の32通りです。