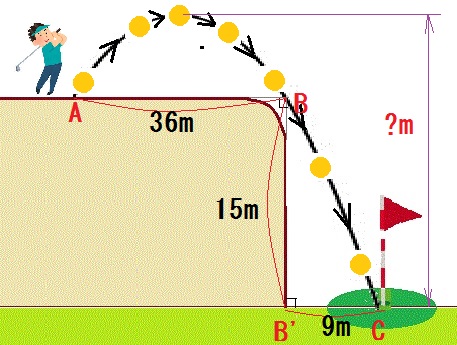
右図のように、よしお君はゴルフボールを打った打ちました。そのボールは最高点に達し、36m(AB)離れた位置で、打ち上げた位置に落ちてきました。
さらに、15m(BB')崖下にあるカップにホールインワンしました。ただし、Bの真下にあるB'からカップの距離は9m(B'C)です。
(ただし、空気摩擦などは考えないとします。)
ここで問題です。
よしお君が打った最高点とゴルフカップの高さの差は何mになるでしょうか。
|
<問題> 右図のように、よしお君はゴルフボールを打った打ちました。そのボールは最高点に達し、36m(AB)離れた位置で、打ち上げた位置に落ちてきました。 さらに、15m(BB')崖下にあるカップにホールインワンしました。ただし、Bの真下にあるB'からカップの距離は9m(B'C)です。 (ただし、空気摩擦などは考えないとします。) ここで問題です。 よしお君が打った最高点とゴルフカップの高さの差は何mになるでしょうか。 |
 |
<正解者一覧表> 順位
name
メール到着日時
備 考
1
源内シンガポール さん
2017/11/1 0:03
長崎県
2
algebra さん
2017/11/1 0:03
神奈川県
3
teki さん
2017/11/1 0:03
大阪府
4
Mr.ダンディ さん
2017/11/1 0:06
大阪府
5
男はつらいよ さん
2017/11/1 0:07
神奈川県
6
ゴンとも さん
2017/11/1 0:11
豊川市
7
kou さん
2017/11/1 0:13
さいたま
8
デアルケ さん
2017/11/1 0:21
三重県紀北町
9
まいすた さん
2017/11/1 0:27
10
朝霞おじ さん
2017/11/1 1:22
埼玉県
11
いぬたこ さん
2017/11/1 3:25
千葉
12
うたねこ さん
2017/11/1 3:43
関東
13
山本フランキーやすかず
2017/11/1 3:45
愛知県かんのんじのおしょさまさん
14
巷の夢 さん
2017/11/1 7:28
神奈川県在住
15
ユートニウム さん
2017/11/1 9:57
16
花田美恵子 さん
2017/11/1 10:20
日本
17
りょうま さん
2017/11/1 10:52
愛媛県
18
いちもく さん
2017/11/1 10:59
立川市
19
お城祭り出店 さん
2017/11/1 18:38
20
マッキー27 さん
2017/11/1 20:07
愛知県
21
NNR4 さん
2017/11/1 21:01
兵庫県
22
スモークマン さん
2017/11/1 22:18
@新倉敷
23
dyslexia さん
2017/11/2 0:42
大阪府
24
次郎長 さん
2017/11/2 7:42
兵庫県
25
やぶコウノトリ さん
2017/11/2 10:55
兵庫県
26
GUTENTAG さん
2017/11/2 11:05
27
阿修羅 さん
2017/11/2 21:42
長野県
28
AKIRA さん
2017/11/2 22:50
愛知県
29
ローリー さん
2017/11/3 12:02
大阪府
30
算数の森 さん
2017/11/3 16:54
兵庫県
31
岡本ボンバーズ さん
2017/11/7 13:03
32
アインズ ウール ゴウン さん
2017/11/8 17:30
ナザリック地下大墳墓
33
たかひろ さん
2017/11/8 23:32
埼玉県