「今月の問題」　第２１９回　（平成２９年１２月）
 
＜問題＞　

 　よしお君は家族で回転ずしを食べに行きました。よしお君は、右図のメニューの中で「まぐろ」２皿と「いくら」２皿と、「えび」と「中とろ」と「サーモン」を１皿以上食べたところ、全摂取カロリーは１４００kcalになりました。

　ここで問題です。
 　よしお君が食べた寿司の合計金額が一番安い場合、その時の合計金額を求めて下さい。

  
１皿の値段（カロリー）については、以下の通りです。
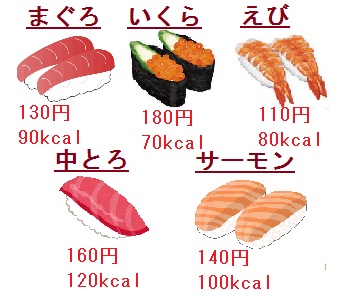
まぐろ（130円、90kcaｌ）、いくら（180円、70kcaｌ）、えび（110円、80kcaｌ）、中とろ（160円、120kcaｌ）、サーモン（140円、100kcaｌ）

 

＜正解者一覧表＞　 　　　　　　　　　　　　　　　　　　　
順位 　　　　ｎａｍｅ　　　 　　メール到着日時 　　 　　備　考　　
　１ kou　さん 2017/12/1　2:46 さいたま　
　２ フランキーひさし　さん 2017/12/1　5:24 　
　３ うたねこ　さん 2017/12/1　5:25 関東　
　４ 鯨鯢(Keigei)　さん 2017/12/1　5:48 　
　５ algebra　さん 2017/12/1　6:29 愛知県　
　６ 男はつらいよ　さん 2017/12/1　6:41 神奈川県　
　７ 巷の夢　さん 2017/12/1　6:48 神奈川県在住　
　８ りさちゃん　さん 2017/12/1　7:38 　
　９ 次郎長　さん 2017/12/1　8:03 兵庫県　
１０ teki　さん 2017/12/1　8:52 大阪府　
１１ ＧＯＧＯＧＩＡＮＴＳ　さん 2017/12/1　9:43 　
１２ ユートニウム　さん 2017/12/1　9:52 　
１３ いぬたこ　さん 2017/12/1　10:10 千葉　
１４ ほかず　さん 2017/12/1　10:12 愛知　
１５ いちもく　さん 2017/12/1　11:24 立川市　
１７ 初芝立命館高校　さん 2017/12/1　15:23 大阪府　
１８ 朝霞おじ　さん 2017/12/1　21:03 埼玉県　
１９ マッキー２７　さん 2017/12/1　21:29 愛知県　
２０ Ｍｒ．ダンディ　さん 2017/12/2　0:46 大阪府　
２１ AKIRA　さん 2017/12/2　11:38 愛知県　
２２ GUTENTAG　さん 2017/12/2　12:58 滋賀県　
２３ たかひろ　さん 2017/12/3　15:55 埼玉県　
２４ 阿修羅　さん 2017/12/3　21:59 長野県小学校教諭　
２５ dyslexia　さん 2017/12/4　9:32 　
２６ striker2981　さん 2017/12/4　14:08 岩手県　
２７ ローリー　さん 2017/12/4　16:52 大阪府　
２８ 観葉植物は室内　さん 2017/12/6　9:56 兵庫県　
２９ りょうま　さん 2017/12/7　15:49 愛媛県　
３０ スモークマン　さん 2017/12/8　22:56 ＠新倉敷　

答えは、２０８０円でした。

[387] やっとこどっこい...^^; 投稿者： スモークマン <12gatu> 投稿日： 2017/12/08(Fri) 23:06  
みなさんと同じく...カロリー単価で考えればいいことに気づけてやっとこさ ^^;
トロ(x:4/3=1.33)＜エビ(y:11/8=1.375)＜サーモン(z:7/5=1.4)
so...
12x+8y+10z=78
6x+4y+5z=39
6*5+4*1+5*1=39 で...
310*2+160*6+110*2+140*2=2080円
最初...2100円と思い込んでました...Orz...

今年もあっと間にすぎちゃいましたけど...
毎月楽しませていただきありがとうございました♪
[386] Re:[385] 素直に 投稿者： teki <12gatu> 投稿日： 2017/12/01(Fri) 13:59  
> 解きました。
>
> 条件を満たすには、エビ、中トロ、サーモンで１０８０kcalが必要。
> エビ、中トロ、サーモンは各々１皿以上必要なので、残り７８０kcalを３種類で達成する必要がある。
> 最も安価な場合は、calあたりのが単価が低い中トロを多く食べた場合なので、これを中心に計算すると、
>
> マグロ２皿、いくら２皿、エビ２皿、中トロ６皿、サーモン２皿の場合が最も安く、
>

２０９０→２０８０　でした。
> １３０×２＋１８０×２＋１１０×２＋１６０×６＋１４０×２＝２０９０円
[385] 素直に 投稿者： teki <12gatu> 投稿日： 2017/12/01(Fri) 13:56  
解きました。

条件を満たすには、エビ、中トロ、サーモンで１０８０kcalが必要。
エビ、中トロ、サーモンは各々１皿以上必要なので、残り７８０kcalを３種類で達成する必要がある。
最も安価な場合は、calあたりのが単価が低い中トロを多く食べた場合なので、これを中心に計算すると、

マグロ２皿、いくら２皿、エビ２皿、中トロ６皿、サーモン２皿の場合が最も安く、

１３０×２＋１８０×２＋１１０×２＋１６０×６＋１４０×２＝２０９０円
[384] 十進Basic で 投稿者： ゴンとも <12gatu> 投稿日： 2017/12/01(Fri) 09:29  
FOR ebi=1 TO 20
FOR chutro=1 TO 20
FOR samon=1 TO 20
IF 90*2+70*2+80*ebi+120*chutro+100*samon=1400 THEN PRINT 2;2;ebi;chutro;samon;130*2+180*2+110*ebi+160*chutro+140*samon
NEXT samon
NEXT chutro
NEXT ebi
END

f9押して

2 2 1 5 4 2090
2 2 2 1 8 2120
2 2 2 6 2 2080・・・・・・(答え)
2 2 3 2 6 2110
2 2 4 3 4 2100
2 2 5 4 2 2090
2 2 7 1 4 2110
2 2 8 2 2 2100
[383] 面白い問題を感謝 投稿者： 次郎長 <12gatu> 投稿日： 2017/12/01(Fri) 08:53  
いつもいつも新しい問題を有難うございます。
今回の問題は簡単に解けそうに見えたので5分ほど睨んでいましたが、勘では解けませんでした。
私は巷の夢様の(x,y,z)を借りると、(2,6,2)(3,2,5)(4,3,4)・・を求め、
(2,6,2)の時に最小になることを求めました。
単価とカロリーとの関係があるので、面白かったです。
今年も残り1か月。今月は寒いとか。
[382] お世話になりました。来年も宜しくお願い申し上げます。 投稿者： 巷の夢 <12gatu> 投稿日： 2017/12/01(Fri) 06:58  
エビ、中トロおよびサーモンの個数をｘ、ｙ、ｚとし二つの方程式
を立て、ｚを消去し、二つのグラフのボーダーから求めました。

吉岡先生、本年も面白い問題をありがとうございました。来年も
期待しておりますので、宜しくお願い申し上げます。
それでは、どうぞご自愛下さい。
[381] 無題 投稿者： やまひさ <12gatu> 投稿日： 2017/12/01(Fri) 05:26  
中トロが
最も単価がひくいので
これを
最大化することで
ケース検討しますた