「今月の問題」 第227回 (平成30年8月)
<問題>
「ビール」を円柱形のジョッキーに注ぐと、液体部分と泡の部分に分かれます。泡は時間がたつと液体になりますが、そのとき、体積は1/3になります。
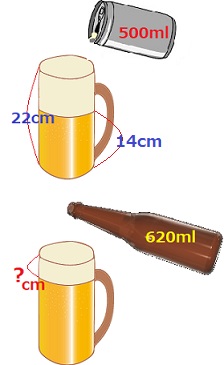
今、深さ22cmの円柱形のジョッキーにビールを500ml注いだら、底から14cmのところまでは液体で、その上はジョッキーの上端まで泡になりました。(1回目)
次に、同じ円柱形のジョッキーに「ビール」を620ml注いだら、ちょうど上端ぴったりで入りきることが出来ました。(2回目)
ここで問題です。
2回目に「ビール」620mlを入れた時の、泡の部分の深さは何cmだったでしょうか。
<注>
①液体が泡になるときは、体積は3倍になります。
②ジョッキーは、断面積が同じ円柱形であると考えてください。
③「ビール」は注ぎ方によって液体と泡の割合が変わるので、同じ容器(ジョッキー)に入るビールの量は、注ぎ方によって変わります。
|
 |
<正解者一覧表>
| 順位 |
name |
メール到着日時 |
備 考 |
| 1 |
algebra さん |
2018/8/1 0:07 |
神奈川県 |
| 2 |
源内シンガポール さん |
2018/8/1 0:08 |
長崎県 |
| 3 |
kou さん |
2018/8/1 0:12 |
さいたま |
| 4 |
朝霞おじ さん |
2018/8/1 0:13 |
埼玉県 |
| 5 |
ゴンとも さん |
2018/8/1 0:16 |
豊川市 |
| 6 |
200日目 さん |
2018/8/1 0:17 |
大阪府 |
| 7 |
男はつらいよ さん |
2018/8/1 0:25 |
神奈川県 |
| 8 |
次郎長 さん |
2018/8/1 1:38 |
暑い兵庫県 |
| 9 |
いぬたけ さん |
2018/8/1 3:27 |
千葉 |
| 10 |
保和 さん |
2018/8/1 3:39 |
愛知 |
| 11 |
りりー山本 さん |
2018/8/1 4:22 |
愛知県 |
| 12 |
鯨鯢(Keigei) さん |
2018/8/1 4:47 |
|
| 13 |
巷の夢 さん |
2018/8/1 5:32 |
神奈川県在住 |
| 14 |
いちもく さん |
2018/8/1 8:33 |
立川市 |
| 15 |
やぶコウノトリ さん |
2018/8/1 10:41 |
兵庫県 |
| 16 |
teki さん |
2018/8/1 12:39 |
大阪府 |
| 17 |
まくわうり さん |
2018/8/1 15:17 |
兵庫県 |
| 18 |
Mr.ダンディ さん |
2018/8/1 20:56 |
大阪府 |
| 19 |
マッキー27 さん |
2018/8/1 23:25 |
愛知県 |
| 20 |
おろおろ さん |
2018/8/2 3:26 |
|
| 21 |
なや さん |
2018/8/2 8:16 |
兵庫県 |
| 22 |
初芝立命館高校 さん |
2018/8/2 12:47 |
大阪府 |
| 23 |
yyyyy さん |
2018/8/2 17:18 |
tokyo |
| 24 |
NNR4 さん |
2018/8/2 20:43 |
兵庫県 |
| 25 |
ひろまな さん |
2018/8/6 11:41 |
茨城県 |
| 26 |
航空アニマル さん |
2018/8/6 19:51 |
東京都26市内大学5年生 |
| 27 |
スモークマン さん |
2018/8/10 22:52 |
暑中お見舞い~m(_ _)m~ |
| 28 |
sue さん |
2018/8/12 13:11 |
筑前州上津役村@福岡県 |
| 29 |
阿修羅 さん |
2018/8/31 19:20 |
長野県 |
答は、2cmでした。
444]
ビールの大瓶は 投稿者:
teki <8gatu>
投稿日: 2018/08/01(Wed) 12:42
一般的に633ccですよね。
計算が楽になるように620ccにしたんですね。
なお、ビール会社の広報によると、一番おいしいビールの注ぎ方は、ビール:泡が7:3らしいです。
[
443]
不注意というか・・・・ 投稿者:
巷の夢 <8gatu>
投稿日: 2018/08/01(Wed) 05:38
題意に沿って立式し、ビール部分が20cmとなったので、
20ですぐに送信、その後正解者掲示板に・・・、ところが
入れない、何故?再度計算するも間違いはない。
おかしいなと思い、問題を再読すると、求めるものは泡の
高さでした。何ともお粗末な一席でした。
[
442]
無題 投稿者:
いわたけ <8gatu> 投稿日:
2018/08/01(Wed) 03:52
ジョッキの底面積をAとして
ビールの液体量に着目し求める高さをYとすると
(14+8/3)A=500
(Y/3+(22-Y))A=620
Aをはらい、Y=2
[
441]
訂正 投稿者:
algebra <8gatu> 投稿日:
2018/08/01(Wed) 00:39
誤 500:650
正 500:620
[
440]
底辺の半径をa 投稿者:
ゴンとも <8gatu>
投稿日: 2018/08/01(Wed) 00:27
円周率を%pi,答えをx(cm)とすると
1回目:a^2*%pi*14+a^2*%pi*8/3=500
2回目:a^2*%pi*(22-x)+a^2*%pi*x/3=620
これらを連立方程式として XMaxima で解くと
part(solve([a^2*%pi*14+a^2*%pi*8/3=500,a^2*%pi*(22-x)+a^2*%pi*x/3=620],[a,x]),2);
a=sqrt(30)/sqrt(%pi),x=2・・・・・・(答え)
[
439]
比 投稿者:
algebra <8gatu> 投稿日:
2018/08/01(Wed) 00:15
求める泡の部分の深さをxcmとすると,
(22-x)+x/3=22-(2/3)x
50/3:(22-(2/3)x)=500:650
x=2(cm)
