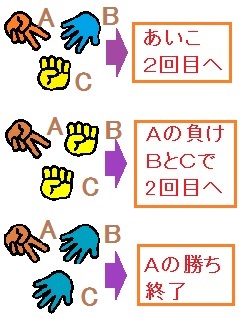
A、B、Cの3人でじゃんけんをします。
一度じゃんけんで負けた人は、以後のじゃんけんから抜けます。
残りが1人になるまでじゃんけんを繰り返し、最後に残ったものを勝者とします。
ただし、あいこの場合も1回のじゃんけんを行ったと数えます。
ここで問題です。3回までのじゃんけんで1人の勝者が決まる確率を求めて下さい。(1回目か2回目か3回目のいずれかで決着がつく確率です。つまり、1回目で決着する確率+2回目で決着する確率+3回目で決着する確率です。)
| <問題> A、B、Cの3人でじゃんけんをします。 一度じゃんけんで負けた人は、以後のじゃんけんから抜けます。 残りが1人になるまでじゃんけんを繰り返し、最後に残ったものを勝者とします。 ただし、あいこの場合も1回のじゃんけんを行ったと数えます。 ここで問題です。3回までのじゃんけんで1人の勝者が決まる確率を求めて下さい。(1回目か2回目か3回目のいずれかで決着がつく確率です。つまり、1回目で決着する確率+2回目で決着する確率+3回目で決着する確率です。) |
 |
<正解者一覧表> 順位
name
メール到着日時
備 考
1
algebra さん
2018/11/1 0:12
神奈川県
2
kou さん
2018/11/1 0:24
さいたま
3
ゴンとも さん
2018/11/1 0:32
豊川市
4
次郎長 さん
2018/11/1 0:35
兵庫県
5
男はつらいよ さん
2018/11/1 0:40
神奈川県
6
鯨鯢(Keigei) さん
2018/11/1 5:05
7
いぬとたこ さん
2018/11/1 5:30
ちば
8
いちもく さん
2018/11/1 8:09
立川市
9
巷の夢 さん
2018/11/1 9:38
神奈川県在住
10
朝霞おじ さん
2018/11/1 10:11
埼玉県
11
マッキー27 さん
2018/11/1 21:27
愛知県
12
ほやす、かえるねこ さん
2018/11/1 3:22
13
teki さん
2018/11/2 13:51
大阪府
14
やぶコウノトリ さん
2018/11/2 14:44
兵庫県
15
たかひろ さん
2018/11/3 0:45
埼玉県
16
nowhereman さん
2018/11/3 9:19
東京都
17
NNR4 さん
2018/11/3 11:40
兵庫県
18
名古屋の殿 さん
2018/11/4 5:38
愛知県
19
Mr.ダンディ さん
2018/11/5 13:17
大阪府
20
スモークマン さん
2018/11/7 11:48
@新倉敷
21
市松 さん
2018/11/12 23:14
答は、23/27 でした。