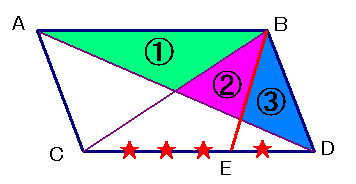
忋恾偺傛偆偵暯峴巐曈宍ABCD偑偁傝傑偡丅
慄暘AD偲俠俛偼暯峴巐曈宍偺懳妏慄偱偡丅
崱丄慄暘CD忋偵揰俤傪俁丗侾偵偲傝丄慄暘BE傪堷偒傑偟偨丅
偙偺帪丄
丂丂丂丂丂丂丂丂(嶰妏宍嘆偺柺愊)
丗 (嶰妏宍嘇偺柺愊) 丗
(嶰妏宍嘊偺柺愊) 偺斾傪媮傔偰壓偝偄丅
丂

|
|
忋恾偺傛偆偵暯峴巐曈宍ABCD偑偁傝傑偡丅 偙偺帪丄 丂 |
丂
摎偊偼丂俆丗俁丗俀偱偡丅
崅嫶偝傫偺夝摎
AD偲BE偺岎揰傪F,AD偲BC偺岎揰傪O偲偟傑偡丅嶰妏宍DEF偲嶰妏宍ABF偼
憡帡偱丄憡帡斾偼1:4傛傝丄DF:AF=1:4丂DF=侾偲偡傞偲AF=4丂AD=俆
AO=OD傛傝丄AO=2.5丂OF=4-2.5=1.5
傛偭偰柺愊斾偼丄AO:AF:FD偲側傝2.5:1.5:1=5:3:2
暿夝傪...CD忋偵G傪BE偲OG偑暯峴偵側傞傛偆偵偲傝傑偡丅
OG暯峴BE傛傝丄CG:GE=CO:OB=1:1丄CG=GE=惎1.5
OG暯峴FE傛傝,OF:FD=GE:ED=惎1.5:惎1=3:2丂AO=OD傛傝丄
柺愊斾偼5:3:2偱偡丅
LION偝傫偺夝摎
AD偲BE偺岎揰傪俥丄2偮偺懳妏慄偺岎揰傪俧偲偡傞偲丄
AB丗DE亖AF丗DF亖係丗侾丄AG丗DG亖1丗1傛傝丄
AG丗GF丗FD亖5丗3丗2
偁偘偝傫丄BossF偝傫丄CRYING DOLPHIN偝傫偺夝摎
慄暘AD偲慄暘BC偺岎揰傪F丄AD偲BE偺岎揰傪G偲偡傞丅
AF:DF亖1:1(暯峴巐曈宍偺惈幙傛傝帺柧)
仮ABG偲仮DEG偱峫偊傞偲4:1偺憡帡宍偺偨傔丄AG:DG=4:1
AF:DF亖5:5丄AG:DG亖8:2 仺 AF:FG:GD亖5:3:2
仮BAF丄仮BFG丄仮BGD偺崅偝偼摨堦偺偨傔丄掙曈偵偁偨傞
AF丄FG丄GD偺斾偑柺愊斾偲側傞丅
傛偭偰丄仮BAF丗仮BFG丗仮BGD亖5:3:2
昹揷偝傫偐傜偺夞摎
崱夞偼俠偱嶌偭偰傒傑偟偨丅
丂丂俠(侽丆侽)丆俢(侾丆侽)
偲偟偰揰俙(倶丆倷)乮亅侾亙倶亝侾丆侽亙倷亝俀乯偺埵抲傪棎悢偵傛偭偰寛傔傑偡丏俙偵偲傕側偄揰俛(倶亄俠俢丆倷)偑寛傑傝丆揰俤偺埵抲偲嘆丆嘇丆嘊偺柺愊偑寛傑傝傑偡丏
丂偙偺帋峴傪侾侽侽侽夞孞傝曉偟丆斾偺暯嬒傪媮傔傑偡丏
丂寢壥偼丆帋峴夞悢偵娭傢傜偢丆忢偵
丂丂1:0.600000:0.400000
偲側傝傑偟偨丏
丂偮傑傝丆摎偼丆
丂丂俆丗俁丗俀
偲側傝傑偡丏
丂偪側傒偵偙偺僾儘僌儔儉偱偼丆嬤帡寁嶼偟偐偟偰偄傑偣傫偺偱丆偨偲偊摎偑偁偭偰偄偨偲偟偰傕丆嶼悢揑乮悢妛揑乯側惓夝偲偼側傝傑偣傫丏
/* 17.C */
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
double rnd(void);
main(){
double x[8],y[8],a[3],b[3],p[3],hen[4],s,menseki[4],wa[4];
int j1,j2,j3,j4,j[4],j1_max=1000;
/* 斾傪媮傔傞 */
x[1]=0; /* C */
y[1]=0;
x[2]=1; /* D */
y[2]=0;
y[5]=0; /* E */
wa[0]=0;
wa[1]=0;
for(j1=1;j1<=j1_max;j1++){
x[0]=2*rnd()-1; /* A */
y[0]=2*rnd();
x[3]=x[0]+x[2]; /* B */
y[3]=y[0]+y[2];
x[4]=x[3]*.5; /* 懳妏慄偺岎揰 */
y[4]=y[3]*.5;
x[5]=.75; /* E */
/* AD:y-Ay=(Dy-Ay)/(Dx-Ax)*(x-Ax) -> (Dx-Ax)(y-Ay)=(Dy-Ay)x-Ax) */
/* -> (Ay-Dy)x+(Dx-Ax)y=Dx*Ay-Ax*Dy */
a[0]=y[0]-y[2];
b[0]=x[2]-x[0];
p[0]=x[2]*y[0]-x[0]*y[2];
/* BE:(By-Ey)x+(Ex-Bx)y=Ex*By-Bx*Ey */
a[1]=y[3]-y[5];
b[1]=x[5]-x[3];
p[1]=x[5]*y[3]-x[3]*y[5];
x[6]=(b[1]*p[0]-b[0]*p[1])/(a[0]*b[1]-a[1]*b[0]); /* AD,BE偺岎揰 */
y[6]=(a[0]*p[1]-a[1]*p[0])/(a[0]*b[1]-a[1]*b[0]);
/* 034, 346, 236 */
for(j2=0;j2<=2;j2++){
j[0]=3*(j2==1)+2*(j2==2);
j[1]=3*(j2!=1)+4*(j2==1);
j[2]=4*(j2==0)+6*(j2>0);
s=0;
for(j3=0;j3<=2;j3++){
j4=(j3+1)%3;
hen[j3]=sqrt((x[j[j3]]-x[j[j4]])*(x[j[j3]]-x[j[j4]])+(y[j[j3]]-y[j[j4]])*(y[j[j3]]-y[j[j4]]));
s+=hen[j3];
}
s*=.5;
menseki[j2]=s;
for(j3=0;j3<=2;j3++){
menseki[j2]*=s-hen[j3]; /* 僿儘儞偺岞幃 */
}
menseki[j2]=sqrt(menseki[j2]);
if(j2>0){
wa[j2-1]+=menseki[j2]/menseki[0];
}
}
printf("%d夞帋峴 -> 1:%lf:%lf\n",j1,wa[0]/j1,wa[1]/j1);
/* 崱傑偱偺暯嬒 */
}
}
double rnd(void){
return((double)rand()/32767.1);
}
mhayashi丂偝傫偺夝摎
俙俢偲俛俠偺岎揰傪俷丄俙俢偲俛俤偺岎揰傪俹偲偡傞丏
嶰妏宍俹俙俛偲嶰妏宍俹俢俤偼憡帡偱偁傝丆
憡帡斾偼係丗侾傛傝柺愊斾偼侾俇丗侾偲側傞丏
偙偙偱嶰妏宍俹俢俤偺柺愊傪侾偲偡傞偲嶰妏宍俹俙俛偺柺愊偼侾俇偲側傞丏
嶰妏宍俹俛俢偲嶰妏宍俹俢俤偵拲栚偡傞偲丆
俹俛丗俹俤亖係丗侾傛傝丆嶰妏宍俹俛俢偺柺愊偼係偲側傝丆
偟偨偑偭偰嶰妏宍俛俤俢偺柺愊偼俆偲側傞丏
偙偙偱嶰妏宍俛俤俢偲嶰妏宍俛俠俢偵拲栚偟偰傒傞偲丆
崅偝嫟捠偱掙曈偺斾偑侾丗係傛傝丆嶰妏宍俛俠俢偺柺愊偼俀侽偲側傞丏
嶰妏宍俷俙俛偲嶰妏宍俛俠俢偺柺愊斾偼丆侾丗俀偱偁傞偙偲偼
柧傜偐側偺偱丆嶰妏宍俷俙俛偺柺愊偼侾侽偲側傞丏
傑偨嶰妏宍俹俙俛偺柺愊偑侾俇側偺偱嶰妏宍俷俹俛偺柺愊偼俇偲側傞丏
嶰妏宍俹俛俢偺柺愊偼
埲忋傛傝丆
嶰妏宍俷俙俛丗嶰妏宍俷俹俛丗嶰妏宍俹俛俢亖侾侽丗俇丗係亖俆丗俁丗俀
偲側傞丏