<問題>
右図を見て下さい。
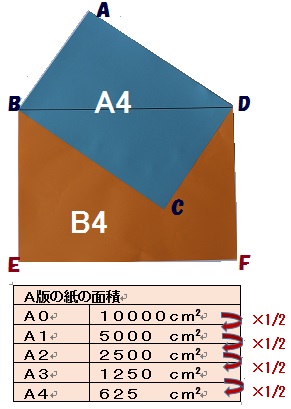
A4サイズの四角形ABCDとB4サイズの四角形BEFDを重ね合わせたところです。A4の対角線をB4の長い辺に重ねると、ぴったし同じ長さになります。
ここで問題です。
B4の用紙の面積は何cm2でになるでしょうか。
ただし、以下の2つのことが分かっています。
① A4の面積は625cm2です。
② A版用紙においてもB版用紙においても、用紙の縦横比は1:√2(白銀比)です。
| <問題> 右図を見て下さい。 A4サイズの四角形ABCDとB4サイズの四角形BEFDを重ね合わせたところです。A4の対角線をB4の長い辺に重ねると、ぴったし同じ長さになります。 ここで問題です。 B4の用紙の面積は何cm2でになるでしょうか。 ただし、以下の2つのことが分かっています。 ① A4の面積は625cm2です。 ② A版用紙においてもB版用紙においても、用紙の縦横比は1:√2(白銀比)です。 |
 |
<正解者一覧表> 順位
name
メール到着日時
備 考
1
algebra さん
2019/3/1 0:07
神奈川県
2
teki さん
2019/3/1 0:08
大阪府
3
ゴンとも さん
2019/3/1 0:08
豊川市
4
kou さん
2019/3/1 0:09
さいたま
5
男はつらいよ さん
2019/3/1 0:13
神奈川県
6
朝霞おじ さん
2019/3/1 0:26
埼玉県
7
Mr.ダンディ さん
2019/3/1 0:45
8
鯨鯢(Keigei) さん
2019/3/1 4:52
9
巷の夢 さん
2019/3/1 5:41
神奈川県在住
10
次郎長 さん
2019/3/1 7:48
花粉の飛び始めた兵庫県
11
いちもく さん
2019/3/1 9:38
立川市
12
ああ春 さん
2019/3/1 9:41
兵庫県
13
GUTENTAG さん
2019/3/1 11:46
滋賀県
14
ひまわひ さん
2019/3/1 12:56
茨城県
15
阿修羅 さん
2019/3/1 21:02
長野県
16
NNR4 さん
2019/3/1 21:07
兵庫県
17
マッキー27 さん
2019/3/1 22:35
愛知県
18
まいすた さん
2019/3/1 22:55
19
いぬ ちこ さん
2019/3/2 9:54
20
何で さん
2019/3/2 17:37
21
市松 さん
2019/3/3 1:11
東京都
22
おかしいな さん
2019/3/3 4:07
23
ほかず さん
2019/3/3 4:09
24
蛸戌 さん
2019/3/3 7:34
25
nowhereman さん
2019/3/4 17:16
tokyo
26
スモークマン さん
2019/3/4 22:43
@新倉敷
27
なや さん
2019/3/5 13:02
兵庫県
28
やぶコウノトリ さん
2019/3/7 13:11
兵庫県
29
AKIRA さん
2019/3/7 13:27
愛知県
30
あめい さん
2019/3/9 23:49
31
西面 敏明 さん
2019/3/10 11:18
兵庫県
32
ひいちゃん さん
2019/3/10 17:35
川口市
33
プロ さん
2019/3/13 13:45
34
岡本ボンバーズ さん
2019/3/22 8:48
35
ハイテク王 さん
2019/3/29 14:12
山口県