安心して老後を過ごすには、2000万円必要であるというニュースがありました。
そこで、よしお君は、毎年100万円ずつ積み立てて、20年間貯金しよう計画しました。利息については、年利率0.3%、1年ごとの複利で加算されます。
ここで問題です。
1.00320=1.06174とすると、20年後の年末における元利合計(貯金額)は、何万円になるでしょうか。(ただし、千円以下の数は切り捨てて下さい)
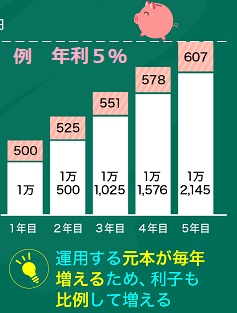
運用する元本に年々増えた利子を組み入れた分に対して、利子が付く計算方法です。
| <問題> 安心して老後を過ごすには、2000万円必要であるというニュースがありました。 そこで、よしお君は、毎年100万円ずつ積み立てて、20年間貯金しよう計画しました。利息については、年利率0.3%、1年ごとの複利で加算されます。 ここで問題です。 1.00320=1.06174とすると、20年後の年末における元利合計(貯金額)は、何万円になるでしょうか。(ただし、千円以下の数は切り捨てて下さい) |
<複利式とは> 運用する元本に年々増えた利子を組み入れた分に対して、利子が付く計算方法です。  |
<正解者一覧表> 順位
name
メール到着日時
備 考
1
市松 さん
2019/9/1 0:11
東京都
2
algebra さん
2019/9/1 0:14
神奈川県
3
マッキー27 さん
2019/9/1 0:20
愛知県
4
kou さん
2019/9/1 0:22
さいたま
5
GOGOGIANTS さん
2019/9/1 0:37
6
男はつらいよ さん
2019/9/1 0:40
神奈川県
7
ゴンとも さん
2019/9/1 0:47
豊川市
8
乙女座 さん
2019/9/1 0:59
9
鯨鯢(Keigei) さん
2019/9/1 6:06
10
巷の夢 さん
2019/9/1 6:10
神奈川県在住
11
戌は蛸 歌猫さん
2019/9/1 6:24
関東
12
保和 さん
2019/9/1 6:48
愛知県
13
朝霞おじ さん
2019/9/1 8:10
埼玉県
14
花田家の一族 さん
2019/9/1 9:22
中部
15
teki さん
2019/9/1 10:00
大阪府
16
Mr.ダンディ さん
2019/9/1 11:30
大阪府
17
GUTENTAG さん
2019/9/1 11:51
滋賀県
18
スモークマン さん
2019/9/1 12:44
@新倉敷
19
いちもく さん
2019/9/1 16:48
立川市
20
山本尚 さん
2019/9/1 16:47
21
まいすた さん
2019/9/1 17:39
22
次郎長 さん
2019/9/2 7:45
そうかそうか兵庫県
23
nowhereman さん
2019/9/3 8:33
TOKYO
24
明日は幼稚園で手品を披露 さん
2019/9/4 6:16
兵庫県
25
NNR4 さん
2019/9/4 21:06
兵庫県
26
なや さん
2019/9/18 9:12
兵庫県
答は、2064万円でした。