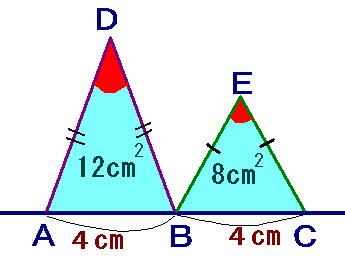
上図のように二等辺三角形ADBと二等辺三角形BECがあります。 二等辺三角形ADBの面積は12cm2であり、二等辺三角形BECの面積は8cm2です。 また、線分AB=4cm、線分BC=4cmです。 この時、 　　　　　　　　∠ADB＋∠BEC  の大きさは何度になるでしょうか。

＜あげさんの考え方＞
詳細は省略しますが、円に内接する四角形の性質を利用して、
角の和が45度になることを導き出し、2倍すると90度が導き出せる。

＜たらおさんの考え方＞　
同様の方法で　ふじさきたつみさん、NobleScarletさん、圭太さん、かつひこさん、高橋　道広さん、Michaelさん、CRYING DOLPHINさん、mhayashiさん他からも解き方を書いていただきました。

 ＡＢ，ＢＣの中点をそれぞれＭ、Ｎとし、四角形ＤＭＮＥを作る。
またＥからＤＭへの垂線の足をＰとする。
面積からＤＭ＝６、ＥＮ＝４でさらにＤＰ＝２である。
すると△ＤＰＥ≡△ＢＮＥとなり、ＥＤ＝ＥＢとなる。
また、∠ＤＥＢ＝∠ＰＥＮ＝９０°なので△ＥＤＢは直角二等辺三角
形。よって∠ＥＢＤ＝４５°。計算で∠ＡＤＢ＋∠ＢＥＤ＝９０°。

＜小杉原啓さんの考え方＞
∠ＡＤＢ＝２α、∠ＢＥＣ＝２βとおき、Ｄ、ＥからＡＣにおろした
垂線の足をＦ、Ｇとおくと、ＤＦ＝６、ＥＧ＝４。
よってtanα＝１／３、tanβ＝１／２。
tan（α＋β）＝（１／３＋１／２）／（１−１／３×１／２）
　　　　　　 ＝1
∴α＋β＝４５
∴２α＋２β＝９０

＜浜田　明巳さんの考え方＞
ワードのマクロで解かれました。
私も、一太郎からWordに乗り換え中です。
こんなプログラムが出来るなんて驚きでした。

Option Explicit

Sub Macro1()
    Dim pi As Double
    Dim rad As Double
    Dim teihen(2) As Double
    Dim takasa(2) As Double
    Dim S(2) As Double
    Dim kotae As Double
    Dim j As Integer
    pi = 4# * Atn(1#)
    rad = pi / 180
    teihen(1) = 4
    teihen(2) = 4
    S(1) = 12
    S(2) = 8
    kotae = 0
    For j = 1 To 2
      takasa(j) = S(j) * 2 / teihen(j)
      kotae = kotae + 2 * Atn((teihen(j) / 2) / takasa(j))
    Next j

    kotae = kotae / rad
    Selection.TypeText Text:="答=" + Str(kotae) + "°"
    Selection.TypeParagraph

End Sub