「今月の問題」　第２４６回　（令和２年３月）
 
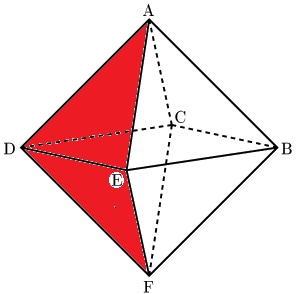
  ＜問題＞　

　右図は、AＦ＝60cmである正八面体ABCDEFです。
　この正八面体をAFを軸として回転させます。


ここで問題です。
側面の△ADEと△DEFが通過するときの体積を求めて下さい。
ただし、円周率は3.14とします。
 
 　
  

＜正解者一覧表＞　
順位 　　　　ｎａｍｅ　　　 　　メール到着日時 　　 　　備　考　　
　１ algebra　さん 2020/3/1　0:05 神奈川県　
　２ 市松　さん 2020/3/1　0:06 東京都　
　３ 男はつらいよ　さん 2020/3/1　0:08 神奈川県　
　４ kou　さん 2020/3/1　0:12 さいたま　
　５ 鯨鯢(Keigei)　さん 2020/3/1　0:13 　
　６ 朝霞おじ　さん 2020/3/1　0:24 埼玉県　
　７ teki　さん 2020/3/1　0:32 大阪府　
　８ ゴンとも　さん 2020/3/1　0:35 豊川市　
　９ 乙女座　さん 2020/3/1　2:24 　
１０ 巷の夢　さん 2020/3/1　6:36 神奈川県在住　
１１ いぬたこ　さん 2020/3/1　7:41 　
１２ スモークマン　さん 2020/3/1　10:42 ＠新倉敷　
１３ フランキー山本　さん 2020/3/1　10:46 　
１４ Mr.ダンディ　さん 2020/3/1　11:03 　
１５ GUTENTAG　さん 2020/3/1　11:43 滋賀県　
１６ チコ勝幸　さん 2020/3/1　12:13 千葉　
１７ まいすた　さん 2020/3/1　12:39 　
１８ NNR4　さん 2020/3/1　14:35 兵庫県　
１９ いちもく　さん 2020/3/1　14:42 立川市　
２０ マッキー２７　さん 2020/3/1　16:25 愛知県　
２１ 花田一族　さん 2020/3/1　17:23 　
２２ 次郎長　さん 2020/3/2　9:39 兵庫県　
２３ K　さん 2020/3/2　12:02 　
２４ 阿修羅　さん 2020/3/4　14:15 長野　
２５ syokyuhsya　さん 2020/3/5　11:05 千葉県　
２６ 　さん 2020/3/　: 　

 

答は　２８２６０ｃｍ3でした

[623] 駄目な私 投稿者： 巷の夢 <3gatu> 投稿日： 2020/03/01(Sun) 06:41  
最初、大きな半径で出来る円錐の体積で送信してしまい、
その後、掲示板にトライしても入れず、おかしいなー。
おかしいのは本人で、そうか小さな半径で出来る円錐を
引いていない・・・・。駄目な私でした。
[622] 平方根を使わずに 投稿者： 鯨鯢(Keigei) <3gatu> 投稿日： 2020/03/01(Sun) 06:22  
円周率が 3.14 なので、平方根を使わずに算数のように解きました。

辺DEを回転して得られる図形は 正方形BCDEの外接円と内接円の間の部分、
外接円の面積は 30×30×3.14＝2826、内接円の面積はその 1/2 です。
なぜなら、面積比は 正方形BCDEの面積と辺の中点を結んでできる正方形の面積比と等しいからです。
従って、外接円と内接円の間の部分の面積は、2826×1/2 です。
△ADEを回転して得られる錐体の体積は、2826×1/2×30/3＝28260×1/2 で、
△FEDを回転して得られる錐体の体積も等しいから、求める体積は２倍して 28260 です。
[621] 図で△ADBでAから 投稿者： ゴンとも <3gatu> 投稿日： 2020/03/01(Sun) 01:11  
線分BDに垂線を下ろし
その足をGとし正八面体を構成する正三角形の
1辺をaとすると△DEBが二等辺三角形よりBD=sqrt(2)*a
ここでBG=BD/2=sqrt(2)*a/2
ここで△AGBで三平方で
AG=sqrt(a^2-(sqrt(2)*a/2)^2)=sqrt(2)*a/2
ここでAG=30よりa=60/sqrt(2)=30*sqrt(2)
ここで正方形BCDEで点Gからの
各正方形の頂点まで距離は30
各正方形の各辺の中点までの距離は30/sqrt(2)=15*sqrt(2)
ここで底面の面積*高さ/3の円錐の体積の差で
30^2*3.14*30/3-450*3.14*30/3
=(900-450)*31.4=14130
この2倍で28260・・・・・・(答え)
[620] 地道に計算 投稿者： algebra <3gatu> 投稿日： 2020/03/01(Sun) 00:22  
正八面体の一辺の長さはa＝30√2　中心から正方形BCDEまでの最大の距離は(√2/2)a
中心から正方形BCDEまでの最小の距離は(1/2)a　よって，求める体積は
π×{(1/2)a^2－(1/4)a^2}×60×1/3＝5πa^2＝5×3.14×1800＝28260(cm3)