今月の問題（時計の問題）

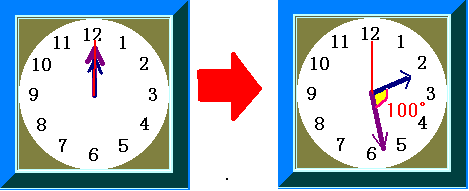
　上左図のように只今の時刻は、短針と長針が重なっている午前０時です。
ある時間が過ぎたら、上右図のように、長針が短針を追い越したあとに２つの針がつくる角度が１００°になったといいます。
　また、その時、秒針はちょうど１２の数字の位置にきています。

　このような現象が、最初に起きるのは、何時何分でしょうか。

＜鈴木さんの解答例＞
長針の１分間に進む角度６度、短針の１分間に進む角度０．５度。よって、時間
（分）をXとして問題を式にすると、
６X－０．５X＝３６０N＋１００
５．５X＝３６０N＋１００
問題より、Xは整数。Nに１から１２を代入、計算して、Xが整数になるのは、N＝４、
X＝２８０。
よって、２８０分→４時４０分

＜ミミズクはくず耳さんの解答＞
Ｈ時Ｍ分とすると、
６Ｍ－（３０Ｈ＋Ｍ／２）＝１００の整数解から
求めました。１５時１００分なんてもの出てきますね。

＜高橋さんの解答＞

短針は１時間に360/12=30度　１分に30/60＝0.5度回転し、長針は1分に360/60=6度回転します。

長針が12の所にある時の時間から、長針が短針に追いついて、100度の差をつけるまで進むこと

を考えます。１分につき　速度の差は6-0.5=5.5度ですから

12時から1時の間のとき　100を割り切れないからだめ

1時から2時の間のとき　　130を割り切れないからだめ...

ということで、分の値が整数であることから、その進む角度は5.5の整数倍要は11の倍数

でなければならない事になります。ということで...

解答

100,130,160,190,220,250...のうち最小の11の倍数は220で、220/5.5=40　よって、4時40分

長針と短針が１００度をつくるのは、１８＋２／１１分　秒針が１２を
さすためには、９／１１分はじめにずれていなくちゃならないので、そ
れを探すと、
　４時２１＋９／１１分に短針と長針が重なり、その１８＋２／１１分
後に１００度をつくるので、たして、４時４０分ちょうどになる。

長針と短針の成す角度が100度になる時刻をX時Y分とする。

午前0時を起点とした場合、X時Y分までに短針が動いた角度は、
360/12×X＋Y/60×30＝30X＋Y/2
であらわされる。

一方、時計上の12の数字を起点として、長針が動いた角度は、
Y/60×360＝6Y
であらわされる。

長針が短針を追い越した後に、長針と短針が作る角度は100度と
なるので、
6Y－（30X＋Y/2）＝100
11Y－60X＝200・・・Ａ
となる。

条件より、長針と短針の成す角度が100度になるとき、秒針は時計上の
12の上に来ているため、Ａの（X、Y）の整数解を求めればよい（（0≦X≦12、
0≦Y＜60）。
このような（X、Y）の整数解は（4、40）となる。

従って、答えは4時40分。

＜浜田さん　の解答＞
Grapes/win 1.9
[Don't Edit]
----------
BGstretchOn BGfile
0
----------
UserFunction
1
min(x,360-x)
----------
y = f(x)
0
----------
0 = f(x,y)
0
----------
Point
7
2 0
P
0
0
1
0 0
1 1 0 1
2 0 2
1 9
!{int(t/60)}時!{t mod 60}分,!{f(arg(A,P,B))}°
-.5Pr
-1.2Pr

0 0
0 1 0 1
2 0 1
0 0
0 0
0 0
1 9
!{t mod 60}
.9Prcos(90-6t)
.9Prsin(90-6t)

0 0
2 1 0 1
2 0 1
1 9
!{int(t/60)}
.7cos(90-t/2)
.7sin(90-t/2)

0 0
3 1 0 1
2 0 1
----------
Segments
2
1 6 1 2 0 2 0
1 7 1 3 0 2 0
----------
paramater
14
1.00000000000000E+0000 0
1.00000000000000E+0002 0
1.00000000000000E+0000 0
1.00000000000000E+0000 0
1.00000000000000E+0000 0
1.00000000000000E+0000 0
1.00000000000000E+0000 0
1.00000000000000E+0000 0
1.00000000000000E+0000 0
2.80000000000000E+0002 0
1.00000000000000E+0000 0
1.00000000000000E+0000 0
0.00000000000000E+0000 0
1.00000000000000E+0000 0
1.00000000000000E+0000 1 1
----------
KakuMode ScanWidth LogMode ThetaMode AreaMode
2 4 2 1 1
DrawMode
1
AfterImageColorNo
2
circleMode
1
----------
ScaleX
Vlow,VHigh
0 440
AxesVisible,ScaleVisible,Svaluevisible
0 0 0
NUmber,Base
7 1.00000000000000E+0000
High,Low
1.50000000000000E+0000 -1.50000000000000E+0000
----------
ScaleY
Vlow,VHigh
0 440
AxesVisible,ScaleVisible,Svaluevisible
0 0 0
NUmber,Base
7 1.00000000000000E+0000
High,Low
1.50000000000000E+0000 -1.50000000000000E+0000
----------
ScaleS
SquareQ AreaRectify PsMesh AxisWidth FontSize
0 0 0 1 18
----------
Yvalue
1.00000000000000E+0000
----------
Iinterval
Svalue Evalue sliceNo
-1.00000000000000E+0000 1.00000000000000E+0000 40
Dfuncno Efuncno AreaQ
1 0 0
----------
Yvalue Function List
9
y1
y2
y3
y4
y5
y6
y7
y8
y9
----------
Panel Position
424 0 48 196 269 365
----------
MEMO SECTION
Style, Color, BGcolor , Size, PositionX, positionY
3 1 0 20 10 10 0
13
問題 '0104
# //Click and you'll start the program.
# a:=0
# t:=0
# while a=0
# draw
# if arg(A,P,0,1)-arg(B,P,0,1)=100 then
# a:=1
# else
# t:=t+1
# endif
# wend
# ---
----------

題意を満たすのが12時のx分後とすれば
5.5x=100+360n
変形して
11x=40(5+18n)
これを満たすのは
n=4+11k　x=40(7+18k)
ところで、12時間=720分で
40(7+18k)≡280(mod720)だから
求める時刻は4：40（12時制）

1分間に長針は6度、短針は0.5度進む。すなわち5.5度角度が開いて
ゆくことになる。
短針に長針が追いつくまでの時間はN時の時には N*30/5.5分かかる。
そこから角度が100度になるまでの時間は100/5.5分後となる。
つまり、求める答えはN時(N*60+200)/11分である。
秒針が12のところを指すという条件から(N*60+200)/11が整数にな
る必要があり、この条件を満たすNの最小値は4である。
N=4を代入すると、4時40分が求める答えとなる。