「今月の問題」 (令和3年2月)
<問題>
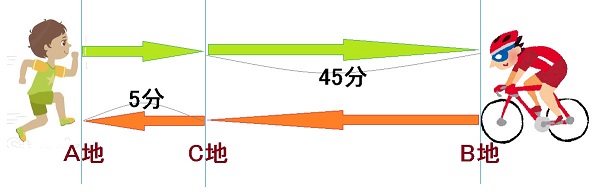
A地点からB地点へ向かう道があります。
よしお君は、一定の早さ時速5kmでA地点からB地点へ歩いて出発しました。
ひさお君は、同時刻に一定の速度で、B地点からA地点に自転車で出発しました。
2人は、途中のC地点ですれ違った後、よしお君はB地点まで45分、ひさお君はB地点まで5分を要してA地点に到着しました。
ここで問題です。
ひさお君は時速何kmで走ったのでしょうか。
|
 |
<正解者一覧表>
| 正解者順位 |
name |
メール到着日時 |
備 考 |
| 1 |
algebra さん |
2021/2/1 0:01 |
神奈川県 |
| 2 |
teki さん |
2021/2/1 0:02 |
大阪府 |
| 3 |
男はつらいよ さん |
2021/2/1 0:07 |
神奈川県 |
| 4 |
量子論 さん |
2021/2/1 0:08 |
京都市中京区 |
| 5 |
GOGOGIANTS さん |
2021/2/1 0:10 |
|
| 6 |
スモークマン さん |
2021/2/1 0:18 |
@新倉敷 |
| 7 |
#719 さん |
2021/2/1 0:19 |
|
| 8 |
乙女座 さん |
2021/2/1 0:32 |
|
| 9 |
kou さん |
2021/2/1 0:55 |
さいたま |
| 10 |
鯨鯢(Keigei) さん |
2021/2/1 4:50 |
|
| 12 |
巷の夢 さん |
2021/2/1 6:10 |
神奈川県在住 |
| 13 |
朝霞おじ さん |
2021/2/1 6:34 |
|
| 14 |
いぬたこ さん |
2021/2/1 7:07 |
|
| 15 |
次郎長 さん |
2021/2/1 7:36 |
兵庫県 |
| 16 |
花田一族 さん |
2021/2/1 8:24 |
|
| 17 |
うたねこ さん |
2021/2/1 8:30 |
関東 |
| 18 |
nowhereman さん |
2021/2/1 9:38 |
東京都 |
| 19 |
山本HISASHI さん |
2021/2/1 13:37 |
|
| 20 |
いちもく さん |
2021/2/1 14:32 |
立川市 |
| 21 |
マッキー27 さん |
2021/2/1 22:32 |
愛知県 |
| 22 |
オケヒット さん |
2021/2/2 2:03 |
|
| 23 |
大阪市の中学受験プロ家庭教師 さん |
2021/2/2 10:32 |
大阪府 |
| 24 |
Mr.ダンディ さん |
2021/2/2 11:23 |
大阪府 |
| 25 |
GUTENTAG さん |
2021/2/3 10:56 |
滋賀県 |
| 26 |
NNR4 さん |
2021/2/3 22:17 |
兵庫県 |
| 27 |
算数バカ さん |
2021/2/4 10:56 |
|
| 28 |
syokyuhsya さん |
2021/2/6 17:19 |
千葉県 |
| 29 |
岡本ボンバーズ さん |
2021/2/12 7:15 |
秋田県 |
| 30 |
なみこ さん |
2021/2/15 23:29 |
|
| 31 |
くらげ さん |
2021/2/17 15:52 |
|
| 32 |
阿修羅 さん |
2021/2/18 15:45 |
長野県小学校教諭 |
答えは、15km/h でした。
[
754]
無題 投稿者:
岡本ボンバーズ <2gatu>
投稿日: 2021/02/12(Fri) 07:59
連立方程式の解けなさと、ひさお君チャリンコのわりにあんまり速くないのねという事実に一瞬焦りましたが、なんとかできました。
[
753]
無題 投稿者:
算数バカ <2gatu>
投稿日: 2021/02/04(Thu) 11:08
C地点で出会うまでの時間を①分とすると、①:5=45:①が成り立つ。よって、内頂と外頂の積を利用すると、①×①=5×45=225=15×15であり、①=15である。よって、5㎞/時×15分=□㎞/時×5分になり、□には15が当てはまる。
[
752]
一見条件が足りない?と思ったが 投稿者:
オケヒット <2gatu>
投稿日: 2021/02/02(Tue) 02:03
スモークマンさんと全く同じ解法でした!
良い問題ですね!
[
751]
図より 投稿者:
№719 <2gatu>
投稿日: 2021/02/01(Mon) 20:45
徒歩で45分かかる距離を自転車では X 分と置くと
徒歩で X分かかるところを 自転車では 5分だから
45 : X = X
: 5
これより X = 15
すなわち
徒歩で60分かかる距離 5kmを自転車では
20分だから自転車の時速は15km
[
750]
出会うまでの時間を a分として 投稿者:
Mr.ダンディ <2gatu>
投稿日: 2021/02/01(Mon) 11:47
出会うまでの時間を a分として
AC間を二人のかかった時間の比 は a:5
CB間を二人のかかった時間の比 は 45:a
これらの比は等しいので
a:5=45:a
解いて a=15
ひさお君のはやさは よしお君の3倍となり
5x3=15(km/時)としました。
[
749]
以前に 投稿者:
teki <2gatu>
投稿日: 2021/02/01(Mon) 10:26
類似問を解いたことがあり、速度比(時間比の逆数)が平方になることを知っていたので、すぐできました。
ただ、初見ではちょっと悩むでしょうね。
見た目は単純なので、舐めると思考停止するような良問です。
[
748]
AB間の距離=x 投稿者:
ゴンとも <2gatu>
投稿日: 2021/02/01(Mon) 09:21
ひさお君の自転車の速度=a(km/h)
よしお君とひさお君が出発してからす合った時間(=すれ違った時間)=t(h)として
Maxima で
part(solve([5*t+a*t=x,5*3/4=x-5*t,a/12=x-a*t],[a,x,t]),1);
a=15・・・・・・(答え),x=5,t=1/4
問題がでることを忘却していて・・・
道であう問題にしては一般的には易問なのかは?
問題文に図があるから1分以内で・・・
[
747]
どこが難しい? 投稿者:
次郎長 <2gatu>
投稿日: 2021/02/01(Mon) 09:11
鯨鯢(Keigei) 様の考え方は私には出来ないととっくに諦めています。
単純に方程式をたてて解ければそれで良いじゃないかとずっと考えて
来ましたが、今回の問題、見た目は超カンタン。
ところが取り組むと、おっとどっこい。
考えていた10倍くらい時間かかりました。
面白かったです。
[
746]
Re:[745]
無題 投稿者:
巷の夢 <2gatu> 投稿日:
2021/02/01(Mon) 06:15
成程、鯨鯢(Keigei) 様のいつもながらのエレガントな
解法には感心させられます。
因みに、小職は方程式で解いてしまいました。
[
745]
無題 投稿者:
鯨鯢(Keigei) <2gatu>
投稿日: 2021/02/01(Mon) 05:40
自転車の速度を徒歩の速度のk倍とすれば、
同じ区間の時間の比は、自転車:徒歩=1:k です。
かかる時間は、AC徒歩=BC自転車 だから、
AC自転車:AC徒歩:BC徒歩=1:k:k^2 になり、
k^2=9
、k=3 になって、自転車の速度は時速15kmです。
地道に...^^;
自転車の速度:x km/時
(AC/(5km/時))分=((5km/時)*45分/x)分
AC/x=5分
x^2=5*5*9
x=5*3=15km/分
♪

