「今月の問題」 (令和3年3月)
過去問を見る
<問題>
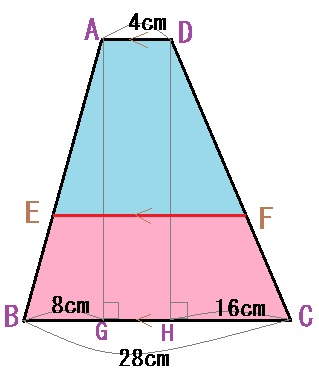
上底4cm、下底28cmの右の台形ABCDがあります。
辺AB上の点Eと辺CDの点FをAD∥EFを満たしながら、線分EFが台形ABCDの面積を二等分するようにとります。
ここで問題です。
線分EFの長さは何cmになるでしょうか。 |
 |
<正解者一覧表>
| 正解者順位 |
name |
メール到着日時 |
備 考 |
| 1 |
量子論 さん |
2021/3/1 0:05 |
京都市中京区 |
| 2 |
男はつらいよ さん |
2021/3/1 0:08 |
神奈川県 |
| 3 |
o さん |
2021/3/1 0:10 |
|
| 4 |
ゴンとも さん |
2021/3/1 0:12 |
豊川市 |
| 5 |
algebra さん |
2021/3/1 0:17 |
神奈川県 |
| 6 |
GOGOGIANTS さん |
2021/3/1 0:18 |
神奈川県 |
| 7 |
次郎長 さん |
2021/3/1 0:22 |
兵庫県 |
| 8 |
マッキー27 さん |
2021/3/1 0:33 |
愛知県 |
| 9 |
Bトレマン さん |
2021/3/1 0:39 |
|
| 10 |
ゆみこちゃん さん |
2021/3/1 0:42 |
|
| 11 |
朝霞おじ さん |
2021/3/1 0:45 |
埼玉県 |
| 12 |
kou さん |
2021/3/1 0:46 |
愛知県 |
| 13 |
乙女座 さん |
2021/3/1 1:01 |
|
| 14 |
鯨鯢(Keigei) さん |
2021/3/1 5:01 |
|
| 15 |
いぬタコ うたねこ さん |
2021/3/1 5:49 |
関東 |
| 16 |
チコかつと花田一族 さん |
2021/3/1 5:56 |
|
| 17 |
巷の夢 さん |
2021/3/1 6:16 |
神奈川県在住 |
| 18 |
ひさし山本 さん |
2021/3/1 6:48 |
|
| 19 |
№719 さん |
2021/3/1 7:39 |
|
| 20 |
teki さん |
2021/3/1 7:54 |
大阪府 |
| 21 |
GUTENTAG さん |
2021/3/1 11:08 |
滋賀県 |
| 22 |
Mr.ダンディ さん |
2021/3/1 11:21 |
大阪府 |
| 23 |
いちもく さん |
2021/3/1 11:56 |
立川市 |
| 24 |
畑仕事 さん |
2021/3/1 13:31 |
兵庫県 |
| 25 |
スモークマン さん |
2021/3/1 13:34 |
@新倉敷 |
| 26 |
保和 さん |
2021/3/1 13:57 |
|
| 27 |
nowhereman さん |
2021/3/1 20:25 |
TOKYO |
| 28 |
syokyuhsya さん |
2021/3/2 9:46 |
|
| 29 |
俵 耕一 さん |
2021/3/2 12:48 |
|
| 30 |
アルファ・ケンタウリ さん |
2021/3/2 19:46 |
京都府小学5年 |
| 31 |
NNR4 さん |
2021/3/2 22:29 |
兵庫県 |
| 32 |
ひまわひ さん |
2021/3/3 10:16 |
|
| 33 |
あめい さん |
2021/3/3 21:28 |
静岡県 |
| 34 |
くらげ さん |
2021/3/7 2:42 |
|
| 35 |
なみこ さん |
2021/3/8 0:24 |
|
| 36 |
大阪の中学受験プロ家庭教師 さん |
2021/3/8 23:42 |
|
| 37 |
オケヒット さん |
2021/3/13 5:06 |
|
| 38 |
阿修羅 さん |
2021/3/15 15:31 |
長野県小学校教諭 |
| 39 |
さん |
2021/3/ : |
|
こたえは、20cmでした
[
766]
Re:[762]
なるほど... 投稿者:
あめい <3gatu>
投稿日: 2021/03/03(Wed) 21:26
> 台形の高さを1として上からx:(1-x)
> 4x+12x^2=(4+28)/4=8
> 3x^2+x-2=(3x-2)(x+1)=0
> x=2/3
> so...24*(2/3)+4=20 ♪
>
> としましたが...
>
>
> 28^2-x^2=x^2-4^2
>
> のアプローチの方がスッキリでしたか ^^☆
同じようなものですが、台形AEFDの2倍=台形ABCDから
2(x^2-4^2)=28^2-4^2という式はxが1か所で好きです。
[
765]
元々は 投稿者:
teki <3gatu>
投稿日: 2021/03/03(Wed) 18:27
ABとCDの延長の交点をPとして、△PAD∽△PEF∽△PBCであり、
条件より
△PEF=(△PAD+△PBC )/2
したがって
EF^2=(AD^2+BC^2)/2
このことから、EF^2は、AD^2とBC^2の平均であると言えます。
[
764]
お久しぶりです。 投稿者:
アルファ・ケンタウリ <3gatu>
投稿日: 2021/03/02(Tue) 19:56
巷の夢さんと同じとき方です。
最近塾や学校の宿題がどうちゃらこうちゃらで、久しぶりの参加となりました。
[
763]
高さ方向の寸法が無い‼ 投稿者:
syokyuhsya <3gatu>
投稿日: 2021/03/02(Tue) 15:35
線分EFの長さをxとし、線分ADと線分EFの距離をh1、線分EFと線分BCの距離をh2とすると、台形AEFDの面積と、台形EBCFの面積が等しいので、(4+x)×h1=(x+28)×h2
x=(28h2-4h1)/(h1-h2) y=h1/h2とすれば、x=(28-4y)/(y-1)
台形AEFDの面積と台形EBCFの面積の和は、 (4+x)×h1+(x+28)×h2=(4+28)(h1+h2)
x=32-(4y+28)/(y+1) 2y^2-3y-2=0 従ってy=2 or -1/2. y>0なので、y=2 よって。x=20
[
762]
なるほど... 投稿者:
スモークマン <3gatu>
投稿日: 2021/03/01(Mon) 14:16
台形の高さを1として上からx:(1-x)
4x+12x^2=(4+28)/4=8
3x^2+x-2=(3x-2)(x+1)=0
x=2/3
so...24*(2/3)+4=20 ♪
としましたが...
28^2-x^2=x^2-4^2
のアプローチの方がスッキリでしたか ^^☆
[
761]
Re:[759]
無題 投稿者:
巷の夢 <3gatu> 投稿日:
2021/03/01(Mon) 10:04
次郎長様
>
巷の夢様、「浮浪の館」へご招待します。今まで不参加に気づきませんでした。
ご招待方どうもありがとうございます。現在かなりの数の
算数・数学問題にトライしており、正解に辿り着くまで時間を
無視して考え込んでしまう性格ですので、この位の数で留めて
擱くのがベストだと思っております。
そんな訳ですので、今回はご容赦頂ければと思います。ご高配の程宜しくお願い申し上げます。
[
760]
ああ見たことあると 投稿者:
せいちゃんだよ~~~ん <3gatu>
投稿日: 2021/03/01(Mon) 09:34
そうだここのサイトの問題だったか
しかも.....
[
759]
無題 投稿者:
次郎長 <3gatu>
投稿日: 2021/03/01(Mon) 08:19
基本は巷の夢さんの考え方だと思うのですが、私は
(28+X)(28-X)=(X+4)(X-4)からX-20を求めました。
tekiさんの
>上底と下底の2乗の平均になる
覚えておきます。
巷の夢様、「浮浪の館」へご招待します。今まで不参加に気づきませんでした。
[
758]
探してみると 投稿者:
teki <3gatu>
投稿日: 2021/03/01(Mon) 08:04
平成15年5月と平成17年5月に同じ問題が出題されてました。
上底と下底の長さが分かれば、計算できるので、あとの条件(下底の分割比)
は不要となります。
[
757]
今回で3回目ですね 投稿者:
teki <3gatu>
投稿日: 2021/03/01(Mon) 07:59
このサイトの過去問に2回、同様の問題がありますね。
上底と下底の2乗の平均になるので、
√((16+784)÷2)=√400=20
で、数秒で答えが出てきます。
なお、8cmと12cmの条件は不要ですね。
[
756]
相似比で・・・・ 投稿者:
巷の夢 <3gatu>
投稿日: 2021/03/01(Mon) 07:29
線分ABとDCを延長した交点をOとすると、三角形OADと三角形
OBCは相似比1:7である。線分EFをXとし相似比の二乗が
面積比という関係を使い、計算するとX=20となりました。
[
755]
座標で 投稿者:
ゴンとも <3gatu>
投稿日: 2021/03/01(Mon) 00:45
A(8,t),B(0,0),C(28,0),D(12,t)とすると
直線AB:y=t*x/8,直線CD:y=-t*(x-28)/16
ここで点E,Fのy座標をsとすると
点E(8*s/t,s),点F((28*t-16*s)/t,s) より
□AEFD=4*(t-s)*(4*t-3*s)/t
□EBCF=4*s*(7*t-3*s)/t
ここで□AEFD=□EBCF
(t-s)*(4*t-3*s)=s*(7*t-3*s) 変形して
(t-s)*(4*t-3*s)-s*(7*t-3*s)=4*t^2-14*s*t+6*s^2
=2*(t-3*s)*(2*t-s)
ここでt>sよりt=3*sより
点Fのx座標-点Eのx座標=(28*t-16*s)/t-8*s/t
=(28*3*s-16*s)/(3*s)-8*s/(3*s)=68/3-8/3=20・・・・・・(答え)

