「今月の問題」　第２５９回　（令和３年４月）　 　　 過去問を見る

　
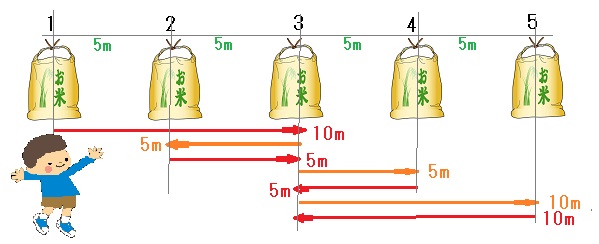
＜問題＞
 　下図は、左端にいるよしお君が５ｍ間隔に置かれたお米を1か所に集めようとしているものです。
３つ目の米袋の位置に集めるには、10+5+5+5+5+10+10＝50mの距離を移動しなければならませんが、他の位置よりは移動する距離が短く済みます。

ここで問題です。
 ５m間隔で３０か所に置かれているお米を1か所に集めます。集める場所によって、一番移動長い距離と一番短い距離の差は何ｍになるでしょうか。

 

＜正解者一覧表＞　 　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１ algebra　さん 2021/4/1　0:23 神奈川県　
　２ o　さん 2021/4/1　0:29 　
　３ 男はつらいよ　さん 2021/4/1　0:30 神奈川県　
　４ kou　さん 2021/4/1　0:36 さいたま　
　５ 乙女座　さん 2021/4/1　1:41 　
　６ 量子論　さん 2021/4/1　2:38 京都市中京区　
　７ 巷の夢　さん 2021/4/1　8:59 神奈川県在住　
　８ 次郎長　さん 2021/4/1　11:13 緊急事態宣言、兵庫県
　９ GUTENTAG　さん 2021/4/1　11:48 滋賀県　
１０ いぬたこ　さん 2021/4/1　13:54 千葉　
１１ 花田勝幸　さん 2021/4/1　13:58 岐阜県　
１２ 山本フランキー　さん 2021/4/1　13:59 　
１３ teki　さん 2021/4/1　15:46 大阪府　
１４ いちもく　さん 2021/4/1　16:52 立川市　
１５ うたねこ　さん 2021/4/1　16:55 関東　
１６ 鯨鯢(Keigei)　さん 2021/4/1　18:50 　
１７ 朝霞おじ　さん 2021/4/1　20:55 埼玉県　
１８ nowhereman　さん 2021/4/1　21:50 ＴＯＫＹＯ　
１９ マッキー２７　さん 2021/4/2　20:20 ＴＯＫＹＯ　
２０ NNR4　さん 2021/4/4　9:43 兵庫県　
２１ syokyuhsya　さん 2021/4/4　19:11 千葉県　
２２ スモークマン　さん 2021/4/21　21:18 ＠新倉敷　
　

 

答えは、２１７５m でした

 

[779] やっとこさ ^^;; 投稿者： スモークマン <4gatu> 投稿日： 2021/04/21(Wed) 21:20   
同じように考えたのになぜか？？？なかなか入れなかったわ ^^;;

3個以上なら、真ん中の位置は動かなくていい分得で、
この問題の場合...最初の1の位置から動いて行くので...
最長...2*(1+2+...+29)
最短...ジグザグで...29+28+...+1
so...1+2+...+29=29*15=435
so...435*5=2175
でしたのね ^^;v
[778] pythonプログラムで解いてみた。 投稿者： syokyuhsya <4gatu> 投稿日： 2021/04/09(Fri) 13:47   
s=5*(i-1)+5*(i-1)*(i-2)+5*(30-i)*(30-(i-1))の間違いでした。
[777] Pythonプログラムで解いてみた。 投稿者： syokyuhsya <4gatu> 投稿日： 2021/04/08(Thu) 19:28   
プログラムは
a=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19.20,21,22,23,24,25,26,27,28,29,30]
added=[]
for i in a:
s=5*(i-1)+5*i*(i-1)+5*(30-i)*(31-i)
added.append(s)
max_s=max(added)
min_s=min(added)
print('最大値=',max_s,'最小値=',min_s)
print('最大値-最小値=',max_s-min_s)
実行すると、2175となりました。
[776] ＨＡＫＩＭＩの定理 投稿者： teki <4gatu> 投稿日： 2021/04/02(Fri) 23:08   
については、元々は「直線間（または平面上）に複数のもの（等間隔とは限りません）が存在し、
これらを一点に集結する場合の総距離を最短にする地点が、長さの中点ではなく個数の中央値で
ある」という位相幾何学上の定理です。

私も、位相幾何学を専門に勉強したわけではないので、詳しく説明できませんが、先般、次郎長
さんがおっしゃってた「浮浪の館」の過去問（第３１１回）にもこれを使った問題があります。
[775] Re:[773] ＨＡＫＩＭＩの定理 投稿者： 巷の夢 <4gatu> 投稿日： 2021/04/01(Thu) 18:47   
teki様

ＨＡＫＩＭＩの定理　初めて聞きました。これからNETで
勉強します。しかし、teki様は色々なことをよくご存じ
ですね。感心しきりです。
[774] 問題文 投稿者： うたねこ <4gatu> 投稿日： 2021/04/01(Thu) 17:00   
問題文で、10+5+5+5+10+10＝50m（左辺は45m）とあり、訳が分からなくなりました。少し考えたらこの数式が間違っているのは理解しましたが。。。
[773] ＨＡＫＩＭＩの定理 投稿者： teki <4gatu> 投稿日： 2021/04/01(Thu) 15:42   
ですね。
一直線上に等間隔で並んだものを一点に集結させる場合の
移動距離の総計が最短となるのは、奇数の場合は中央の地点に、
偶数の場合は、中央の２点間のどこかに集結させる場合であり、
移動距離の総計が最長となるのは、両端に集結させる場合なので
この３つのケース（運ぶ人の移動距離を考えると両端は区別）で
最長が、４３５０ｍ、最短が１５、１６点間に集結させる場合で
２１７５ｍとなりました。
結局、どの場合も、運ぶ人の移動距離は、「最短＝最長/2」になりますね。
なぜ、こうなるかは、よくわかりませんが・・・・。
[772] 無題 投稿者： 山本フランキー <4gatu> 投稿日： 2021/04/01(Thu) 14:01   
15番か16番かどっちが最短か、時間を食いました。問題の意味を理解するのに苦労しました。
[771] 計算間違い、勘違い 投稿者： 次郎長 <4gatu> 投稿日： 2021/04/01(Thu) 11:33   
私も似たようなものです。
どこかにもやもやが残っているものの面白い問題でした。
私は５ｍを１ｍで考えたのに、最後に５倍するのを忘れ、
３時間くらい余分に時間がかかりました。
コロナで憂鬱です。
[770] 地道に階差数列で・・・・ 投稿者： 巷の夢 <4gatu> 投稿日： 2021/04/01(Thu) 09:12   
上手い方法が思い浮かばず、袋の数を3,4,5&6まで書き出し、
最短と最長の差を出して、5ずつ増加することから階差数列で
解きました。

　量子論様のおっしゃるように「最短＝最長/2」が成立する
ように思います。
　algebra様のように16番目が最短と決めきれず、時間がかかってしまいました。
[769] いつも半分？ 投稿者： 量子論 <4gatu> 投稿日： 2021/04/01(Thu) 03:03   
最長距離は「１番目に集める」はいいとして、
最短距離は「総数が奇数個ならど真ん中の位置」、
「偶数個なら中央付近で１番目から見て遠い方」
に集めるのではと、直観的に思ったのですが。

いくつか特定の場合しか調べてませんが、
偶奇いずれの場合でも「最短＝最長/2」が
成立するような気がするのですが、本当なら
面白いですね。
[768] Σの公式で 投稿者： algebra <4gatu> 投稿日： 2021/04/01(Thu) 00:48   
最大距離は1番目で，(1+2+・・・+29)×2×5＝1/2×29×30×2×5＝4350(m)
最小は16番目で、{15＋(1+2+・・・+14)×4}×5＝(15＋1/2×14×
15×4)×5＝2175(m)
よって，4350－2175＝2175(m)