「今月の問題」　第２６０回　（令和３年５月）　 　　 過去問を見る

　
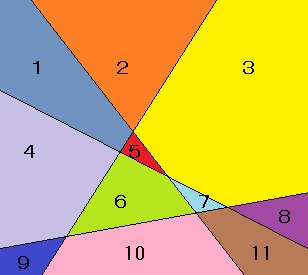
＜問題＞
 　　
平面上に何本かの直線があって、どの2本も平行ではなく、また、どの３本の直線も同一の点で交わらないように書くようにします。
　この条件で４本の直線を書くと、右図のように、これらの直線で１１個の平面に分けられます。


ここで問題です。
 直線の数を６本に増やすと分けられる平面の数は何個になるでしょうか。

＜正解者一覧表＞　 　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１ 源内シンガポール　さん 2021/5/1　0:01 長崎県　
　２ algebra　さん 2021/5/1　0:02 神奈川県　
　３ マッキー２７　さん 2021/5/1　0:03 愛知県　
　４ 男はつらいよ　さん 2021/5/1　0:04 神奈川県　
　５ kou　さん 2021/5/1　0:05 さいたま　
　６ 乙女座　さん 2021/5/1　0:08 　
　７ 次郎長　さん 2021/5/1　0:09 兵庫県　
　８ 鯨鯢(Keigei)　さん 2021/5/1　0:15 　
　９ 量子論　さん 2021/5/1　3:01 京都市中京区　
１０ 朝霞おじ　さん 2021/5/1　4:47 埼玉県　
１１ 巷の夢　さん 2021/5/1　6:11 神奈川県在住　
１２ いぬたこ・うたねこ　さん 2021/5/1　6:31 関東　
１３ 花田勝幸　さん 2021/5/1　6:36 　
１４ 保和フランキー　さん 2021/5/1　6:55 愛知　
１５ syokyuhsya　さん 2021/5/1　9:30 千葉県　
１６ GUTENTAG　さん 2021/5/1　11:45 滋賀県　
１７ Mr.ダンディ　さん 2021/5/1　13:26 大阪府　
１８ いちもく　さん 2021/5/1　13:29 立川市　
１９ あめい　さん 2021/5/1　13:37 静岡県　
２０ 室内猫　さん 2021/5/1　15:22 兵庫県　
２１ teki　さん 2021/5/1　19:09 大阪府　
２２ ゴンとも　さん 2021/5/1　20:08 豊川市　
２３ o　さん 2021/5/1　20:50 　
２４ アルファ・ケンタウリ　さん 2021/5/1　23:10 京都府小学6年　
２５ NNR4　さん 2021/5/2　10:04 兵庫県　
２６ nowhereman　さん 2021/5/2　10:05 ＴＯＫＹＯ　
２７ 大阪市の中学受験プロ家庭教師　さん 2021/5/2　23:30 　
２８ くらげ　さん 2021/5/6　20:03 　
２９ カルダノ　さん 2021/5/25　22:54 群馬　
　

 

答えは２２個でした。

 

[785] Ｎ個に分割したものを 投稿者： teki <5gatu> 投稿日： 2021/05/01(Sat) 19:15   
新たに、全ての分割線と交わるように直線を引けば、分割個数はＮ＋１個増えることになる。
よって、最初の１個を足して、求める数＝１＋∑Ｎとなるので、６本の場合、１＋∑６＝２２個。
[784] 別解 投稿者： 鯨鯢(Keigei) <5gatu> 投稿日： 2021/05/01(Sat) 06:59   
ｎ本目の直線をかいたときに、
それまでの直線と(n－1)ヶ所で交わり、
領域はｎ個増えるので、
領域の数 と 直線の数＋交点の数 の差は
直線の数に関わらず一定です。
直線が０本のときは
領域の数＝1 ，直線の数＋交点の数＝0 だから、
領域の数＝直線の数＋交点の数＋1 です。
直線がｎ本の場合は、領域の数＝n＋nＣ2＋1 です。
直線が６本の場合は、
領域の数＝6＋6Ｃ2＋1＝6＋15＋1＝22 です。
[783] 無題 投稿者： うたねこ <5gatu> 投稿日： 2021/05/01(Sat) 06:38   
答えは数列的にすぐ出せるが実際に図に書こうとすると結構難しい
[782] ３本から始め・・・・ 投稿者： 巷の夢 <5gatu> 投稿日： 2021/05/01(Sat) 06:19   
地道に３本で７個、４本で１１個、そうか直前の本数による
個数に次の本数を加えれば良いのか・・・、これで５本なら
１６個、６本なら２２個となるのでした。
[781] 有名な問題ですね 投稿者： 鯨鯢(Keigei) <5gatu> 投稿日： 2021/05/01(Sat) 00:20   
最初に1つの平面、
1本目の直線で ＋1 個、
2本目の直線で ＋2 個、
3本目の直線で ＋3 個、
4本目の直線で ＋4 個、
5本目の直線で ＋5 個、
6本目の直線で ＋6 個、
よって、1＋1＋2＋3＋4＋5＋6＝22個です。
ｎ本の直線では 1＋n(n＋1)/2 個です。
[780] 漸化式 投稿者： algebra <5gatu> 投稿日： 2021/05/01(Sat) 00:17   
n本の直線によって分けられる部分の個数をAnとすると，
A1＝2，An+1＝An＋(n＋1) これから，An＝1/2(n^2＋n＋2)
よって，A6＝22