「今月の問題」 (令和3年6月)
過去問を見る
<問題>
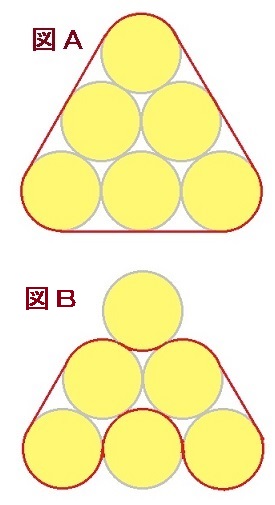
半径15cmの円が6個、右図のように並んで接しています。
この時、図Aと図Bの赤い線の長さを比べてみました。円周率を3で計算するとちょうど同じ長さ(270cm)になるようです。
ここで問題です。
直円周率を3.14として計算すると図Aと図Bの長さの違いは何mmになるでしょうか。
|
 |
<正解者一覧表>
| 正解者順位 |
name |
メール到着日時 |
備 考 |
| 1 |
algebra さん |
2021/6/1 0:07 |
神奈川県 |
| 2 |
男はつらいよ さん |
2021/6/1 0:08 |
神奈川県 |
| 3 |
o さん |
2021/6/1 0:09 |
|
| 4 |
kou さん |
2021/6/1 0:21 |
さいたま |
| 5 |
乙女座 さん |
2021/6/1 0:27 |
|
| 6 |
朝霞おじ さん |
2021/6/1 1:16 |
埼玉県 |
| 7 |
ゴンとも さん |
2021/6/1 4:06 |
豊川市 |
| 8 |
鯨鯢(Keigei) さん |
2021/6/1 4:36 |
|
| 9 |
うたねこ さん |
2021/6/1 5:35 |
関東 |
| 10 |
いぬたこ さん |
2021/6/1 5:39 |
千葉 |
| 11 |
ひさしかつ さん |
2021/6/1 5:42 |
|
| 12 |
巷の夢 さん |
2021/6/1 6:09 |
神奈川県在住 |
| 13 |
花田一族 さん |
2021/6/1 6:28 |
岐阜 |
| 14 |
マッキー27 さん |
2021/6/1 6:33 |
愛知県 |
| 15 |
量子論 さん |
2021/6/1 7:48 |
京都市中京区 |
| 16 |
いちもく さん |
2021/6/1 8:05 |
立川市 |
| 17 |
保和 さん |
2021/6/1 8:45 |
尾張 |
| 18 |
小松菜 さん |
2021/6/1 9:32 |
兵庫県 |
| 19 |
じゃがいも さん |
2021/6/1 9:32 |
兵庫県 |
| 20 |
syokyuhsya さん |
2021/6/1 10:20 |
千葉県 |
| 21 |
Mr.ダンディ さん |
2021/6/1 11:06 |
大阪府 |
| 22 |
GUTENTAG さん |
2021/6/1 15:04 |
滋賀県 |
| 23 |
nowhereman さん |
2021/6/1 15:07 |
TOKYO |
| 24 |
スモークマン さん |
2021/6/1 22:32 |
@新倉敷 |
| 25 |
次郎長 さん |
2021/6/3 0:39 |
コロナ治まらぬ兵庫県 |
| 26 |
teki さん |
2021/6/3 3:19 |
大阪府 |
| 27 |
オケ さん |
2021/6/8 11:30 |
|
答えは、56mm でした。
[
794]
接点のなす角度 投稿者:
syokyuhsya <7gatu>
投稿日: 2021/06/03(Thu) 18:38
接点のなす角度を足して360°何個分に相当するか調べればいいのですね。
[
793]
単位を間違えていました。 投稿者:
syoshimsya <7gatu>
投稿日: 2021/06/03(Thu) 15:21
単位をミリとセンチで間違えていました。如何しても、正解認証されないので、おかしいなと思っていました。
[
792]
私は毎週土曜日のも忘れるぐらいです 投稿者:
No.719 <7gatu>
投稿日: 2021/06/03(Thu) 11:52
接点と接点を結ぶ直線は直径に等しいから
Aの赤線は 直径6個分と円周1個分で270
これとBの赤線とは等しいのだから
Bは直径2個分と円周 1.5個分と 5/6 個分で 270
これらを円周率 3.14で計算すれば
B-A= -120 + 125.6
=5.6
[
791]
私も 投稿者:
teki <7gatu>
投稿日: 2021/06/03(Thu) 10:15
すっかり忘れてました。
ボケちゃ、ダメですね。
わたしゃ、スモークマンさんと同様にAの周長を計算しましたが、
Bの周長については、計算していません。
直線部と曲線部(円周の一部)に分けて考えれば、Bの曲線部は、
円周の7/3個であることが、わかりますので・・・.
[
790]
今月はすっかり失念してましたわ~m(_
_)m~ 投稿者:
次郎長 <7gatu> 投稿日:
2021/06/03(Thu) 00:57
すっかり忘れてました。もう6月なんですね。
[
789]
先月はすっかり失念してましたわ~m(_
_)m~ 投稿者:
スモークマン <7gatu>
投稿日: 2021/06/01(Tue) 22:32
Aの円(円周3*30=90)は...(270-3*60)/90=1個
Bの円...(270-2*30)/90=7/3個
so...
(7/3-1)*30*10*(3.14-3)=4*14=56
♪
[
788]
内容の深い問題ですね・・・ 投稿者:
巷の夢 <7gatu>
投稿日: 2021/06/01(Tue) 06:14
吉岡先生
お世話になります。この様に深く考えたことが無かったので
非常に興味深い問題で驚きました。頭の訓練にもなるし、今後とも
この様な問題で楽しませて頂けるとと思います。
宜しくお願い申し上げます。
[
787]
半径をrとして、 投稿者:
鯨鯢(Keigei) <7gatu>
投稿日: 2021/06/01(Tue) 04:43
半径をrとして、
図Aは (12+2π)r ,図Bは (4+14π/3)r
その差は (-8+8π/3)r=(8r/3)(-3+π)
です。
r=15,π=3.14 とすれば、40×0.14=5.6 、56mm です。
[
786]
図Aで円の半径をrとして 投稿者:
ゴンとも <7gatu>
投稿日: 2021/06/01(Tue) 04:03
円の中心から赤い線に垂線を下ろすと
2*r*3+4*r*3=270 より r=15
ここで3を3.14として
2*15*3+4*15*3.14=274.2・・・・・・(1)
図Bも円の半径を15として円の中心から赤い線に垂線を下ろすと
4*15+2*15*((210*2+180+90*2+60)/360)*3.14=279.8 これと(1)とより
図B-図A=279.8-274.2=5.6cm より 56mm・・・・・・(答え)

