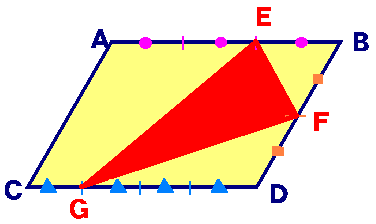
上図のような平行四辺形ABCDがあります。 この平行四辺形の中に、三角形EFGをつくりました。 　ただし、点ＥはＡＢの三等分した所であり、点ＦはＢＤを二等分した所、点ＧはＣＤを４等分した所です。 　この時、三角形EFGの面積は、１３ｃｍ２になったそうです。 　さて、平行四辺形ABCDの面積は何ｃｍ２でしょうか。

＜Marr1982　さんの解答＞

台形EBDGはABDCの２４分の１３
さらに三角形EBFはABDCの12分の1、
そして三角形FDGはABDCの16分の３
よって三角形EFG分のABDC＝24分の３−12分の１−16分の３
＝４８分の１３より、平行四辺形ABCD＝４８平方センチメートル

この解答は、「大豪院邪鬼」さん、「トド３号」さん、「巷の夢」さん、「浜田明巳」さん、「薄袋の人」さん、「ｍｈａｙａｓｈｉ」さん　他　多数のからも頂きました。

＜ＢｏｓｓＦ　さんの解答＞

ＡＢの三等分点のA寄りの点をH,
FDに平行でGを通る直線とABの交点をIとすると
△EFG=△EFIであり、
HI=GD=3/4ABだから、IE=(3/4+1/3)AB=13/12AB
∴△EFG=13/12x1/2x1/2□ABCD=13/48□ABCD
すなわち□ABCD=48

＜ミミズクはくず耳　さんの解答＞

いそいでいるときは、適当な長方形（12*10)
にして計算すると
長方形：三角形＝120:32.5
になったので、13*120/32.5 = 48
と出しました。
ちょっとずるですね

＜高橋　道広さん、圭太さんの解答＞
AB=12とします
EFの延長とCDの延長との交点をHとすると、三角形BEFと三角形DHFが
合同で、DH=EB=12*1/3=４　また、GD=12*3/4=9より、　GH=13
三角形EGH=2*三角形EFG=2*13=26　（上の合同からEF=FHより)
三角形ACD:三角形EGH=CD:GH=12:13から　三角形ACD=24
平行四辺形ABCD=48
(26の面積から　台形EBDG=26　この台形は上底と下底の和が13なの
で、上底と下底の和が24の台形ABCDは26*24/13=48でもいいですね）

＜ふじさきたつみ　さんの解答＞

 ＡＢ＝１２，ＢＤ＝２としたら、△ＥＦＧ＝１３／２，平行四辺形ＡＢ
ＣＤ＝２４となる。実際はその２倍だから、４８平方ｃｍが答えです。

[opinion] Ｆから、ＡＢに平行な線を引いて、ＥＧとの交点をＨとしたら、ＦＨ＝
１３／２となることをつかったけど、そんな必要もないですね。

＜CRYING DOLPHIN　さんの解答＞

三角形ＥＦＢを、点Ｆを中心としてＦＢとＦＤが一致するまで回転させ、
移動後の点ＥをＥ'とすると、三角形ＥＦＧは三角形ＥＧＥ'の面積の半分で、
三角形ＥＧＥ'と平行四辺形の面積比はＧＥ'：２ＣＤ＝１３：２４となることから
解きました。