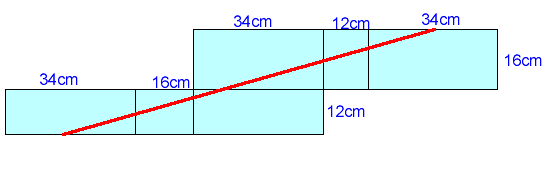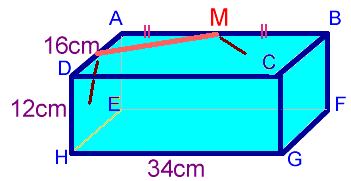
上図のように、縦１６ｃｍ、横３４ｃｍ、高さ１２ｃｍの直方体の箱があります。 この箱を、点Ｍ（ＡＢの中点）から、赤いリボンをまいてデコレーションしたいと思います。 直方体の６面全てを通り、点Ｍに戻る最短の長さを求めたいと思います。 ただし、赤いリボンは、点Ｍから辺ＡＤ上→辺ＥＨ上→辺ＨＧ→辺ＣＧ上→辺ＢＦ上→点Ｍの順番にまいていくものとします。 この時、赤いリボン  の長さは何ｃｍになるでしょうか。 　 （※注意） 青色の条件を加えさせて頂きました。この条件がなければ私が答えと考えていた美しい数字にはならない事が分かりました。 　自分自身の力のなさを痛感しています。この条件でよいのか自信はありませんが、アドバイスのほど宜しくお願いいたします。

＜解答＞
答えは以下の図のように、展開図を書けば、赤い線分の部分１００ｃｍになります。

青い条件を入れると、7:24:25の直角三角形が見えてきます。
私はこれしか思いつかなかったのです。あしからず・・・・・。

しかしながら、最初に出題した青い条件がなければ、１００ｃｍより短くなることが明らかになりました。
でも、私の愚鈍な頭では、答えを見つけられなくて情けなく思っています。
ただ、いろいろな方の回答から、９０ｃｍ前後になることがわかりました。その回答を示したいと思います。
（その他の方からも、どうように同様な回答を寄せていただきました。本当に感謝！感謝！です。私自身の力のなさを実感したのと同時に、数学の奥の深さを感じることができてうれしかったです。）

＜信三さんより＞
私の８８．１９９ｃｍがどうしてできるか御説明しましよう。
Mから辺ＡＤへ、できるだけDの近くへリボンを延ばします。その長さは３平方の計算
で、２３．３４５ｃｍになります。
隣の１６＊１２の面は、できるだけ小さな三角形で通り抜けて、次の長い長方形に入り
ます。
ここは細長い長方形を二つ越して辺FGの上で、できるだけFに近いところへリボンを延ば
します。２８cmと３４cmの長方形の
斜辺で、４４．０４５cmになります。
頂点Fの周りをできるだけ小さな三角形で回り、最後の長い長方形へ入ります。
頂点Fの近くから終点への長さは２０．８０９cmになります。
以上の３個の長さの合計は８８．１９９cmになります。


＜ヒサノッチさんより＞
62√2≒87.68 cm
もしM⇒AD⇒DH⇒HG⇒FG⇒BF⇒M
の順に各辺を横切った場合を考慮すると、もっと短くて済む様なのです。
最初、同じようにこの順での直線を展開図上で引いてその長さを求め
ようとしていた所、あとで途中で線が分断する事に気が付きました。
過去2回お送りした解答は、その事に気付かずにメールしたものでした(^^;;;)。
しかし、分断しない様に、多少迂回したとしても、その量は大した事は無く、
少なくとも100cmは下回りそうです。
それでは、この経路を辿った時の最小値はいくらか？となりますが、
これは各頂点を少しだけずらして面を通るようにすれば良い、というだけ
の為、正確な値を算出する事は出来そうにありません。
っていうのが、私の意見なのですが、どんなもんでしょうか？